Errores tipo I y tipo II: los errores inevitables en la optimización

Los errores de tipo I y tipo II ocurren cuando detecta erróneamente a los ganadores en sus experimentos o no los detecta. Con ambos errores, terminas optando por lo que parece funcionar o no. Y no con los resultados reales.

La mala interpretación de los resultados de las pruebas no solo da como resultado esfuerzos de optimización equivocados, sino que también puede descarrilar su programa de optimización a largo plazo.

¡El mejor momento para detectar estos errores es incluso antes de cometerlos! Entonces, veamos cómo puede evitar encontrarse con errores de tipo I y tipo II en sus experimentos de optimización.

Pero antes de eso, veamos la hipótesis nula… porque es el rechazo erróneo o el no rechazo de la hipótesis nula lo que provoca los errores tipo I y tipo II .

La hipótesis nula: ​H0

Cuando plantea la hipótesis de un experimento, no salta directamente para sugerir que el cambio propuesto moverá una determinada métrica.

Comienza diciendo que el cambio propuesto no afectará en absoluto a la métrica en cuestión, que no están relacionados.

Esta es su hipótesis nula (H0). H0 es siempre que no hay cambio. Esto es lo que crees, por defecto... hasta que (y si) tu experimento lo refuta.

Y tu hipótesis alternativa (Ha o H1) es que hay un cambio positivo. H0 y Ha son siempre opuestos matemáticos. Ha es aquella en la que espera que el cambio propuesto marque la diferencia, es su hipótesis alternativa, y esto es lo que está probando con su experimento.

Entonces, por ejemplo, si quisiera ejecutar un experimento en su página de precios y agregarle otro método de pago, primero formularía una hipótesis nula que dijera: El método de pago adicional no tendrá impacto en las ventas. Su hipótesis alternativa diría: El método de pago adicional aumentará las ventas.

Ejecutar un experimento es, de hecho, desafiar la hipótesis nula o el statu quo.

Los errores de tipo I y tipo II ocurren cuando se rechaza erróneamente o no se rechaza la hipótesis nula.

Comprender los errores de tipo I

Los errores de tipo I se conocen como falsos positivos o errores alfa.

En una instancia de error de tipo I de prueba de hipótesis, su prueba de optimización o experimento * PARECE SER EXITOSO * y usted (erróneamente) concluye que la variación que está probando está funcionando de manera diferente (mejor o peor) que la original.

En los errores de tipo I, ve subidas o bajadas, que son solo temporales y probablemente no se mantendrán a largo plazo , y terminan rechazando su hipótesis nula (y aceptando su hipótesis alternativa).

El rechazo erróneo de la hipótesis nula puede ocurrir por varias razones, pero la principal es la práctica de mirar a escondidas (es decir, mirar los resultados en el ínterin o cuando el experimento aún se está ejecutando). Y llamando a las pruebas antes de que se alcance el criterio de parada establecido.

Muchas metodologías de prueba desalientan la práctica de mirar a escondidas, ya que mirar los resultados provisionales podría llevar a conclusiones erróneas que generarían errores de tipo I.

Así es como podría cometer un error de tipo I:

Suponga que está optimizando la página de destino de su sitio web B2B y tiene la hipótesis de que agregarle insignias o premios reducirá la ansiedad de sus prospectos, lo que aumentará su tasa de llenado de formularios (lo que resultará en más clientes potenciales).

Entonces, su hipótesis nula para este experimento es: agregar insignias no tiene ningún impacto en los formularios que se completan.

El criterio de finalización para un experimento de este tipo suele ser un período determinado y/o después de que se produzcan X conversiones en el nivel de significación estadística establecido. Convencionalmente, los optimizadores intentan alcanzar la marca de confianza estadística del 95 % porque le deja un 5 % de posibilidades de cometer el error de tipo I que se considera lo suficientemente bajo para la mayoría de los experimentos de optimización. En general, cuanto mayor sea esta métrica, menores serán las posibilidades de cometer errores de tipo I.

El nivel de confianza al que aspira determina cuál será su probabilidad de obtener un error de tipo I (α).

Entonces, si apunta a un nivel de confianza del 95%, su valor para α se convierte en 5%. Aquí, acepta que hay un 5% de posibilidades de que su conclusión sea incorrecta.

Por el contrario, si va con un nivel de confianza del 99 % con su experimento, su probabilidad de obtener un error de tipo I se reduce al 1 %.

Digamos, para este experimento, que se vuelve demasiado impaciente y en lugar de esperar a que finalice su experimento, mira el tablero de su herramienta de prueba (¡mira!) solo un día después. Y nota un aumento "aparente": que su tasa de llenado de formularios ha aumentado un 29,2 % con un nivel de confianza del 95 %.

Y BAM...

… detienes tu experimento.

… rechazar la hipótesis nula (que las insignias no tuvieron impacto en las ventas).

… acepte la hipótesis alternativa (que las insignias impulsaron las ventas).

… y corre con la versión con las insignias de los premios.

Pero a medida que mide sus clientes potenciales durante el mes, encuentra que el número es casi comparable con lo que informó con la versión original. Después de todo, las insignias no importaban tanto. Y que la hipótesis nula probablemente fue rechazada en vano.

Lo que sucedió aquí fue que terminó su experimento demasiado pronto y rechazó la hipótesis nula y terminó con un falso ganador: cometió un error de tipo I.

Evitar errores de tipo I en sus experimentos

Una forma segura de reducir sus posibilidades de cometer un error de tipo I es tener un nivel de confianza más alto. Un nivel de significación estadística del 5 % (que se traduce en un nivel de confianza estadística del 95 %) es aceptable. Es una apuesta que la mayoría de los optimizadores harían con seguridad porque, aquí, fallarás en el improbable rango del 5%.

Además de establecer un alto nivel de confianza, es importante ejecutar las pruebas durante el tiempo suficiente. Las calculadoras de duración de la prueba pueden decirle durante cuánto tiempo debe ejecutar su prueba (después de tener en cuenta cosas como un tamaño de efecto específico, entre otros). Si deja que un experimento siga su curso previsto, reduce significativamente sus posibilidades de encontrar el error de tipo 1 (dado que está utilizando un nivel de confianza alto). Esperar hasta que alcance resultados estadísticamente significativos garantiza que solo hay una probabilidad baja (generalmente del 5 %) de que rechazó la hipótesis nula erróneamente y cometió un error de tipo I. En otras palabras, use un buen tamaño de muestra porque es crucial para obtener resultados estadísticamente significativos.

Ahora, eso fue todo acerca de los errores de tipo I que están relacionados con el nivel de confianza (o importancia) en sus experimentos. Pero también hay otro tipo de error que puede colarse en sus pruebas: los errores de tipo II.

Comprender los errores de tipo II

Los errores de tipo II se conocen como falsos negativos o errores Beta.

En contraste con el error de tipo I, en el caso de un error de tipo II, el experimento *PARECE SER FALLIDO (O NO CONCLUYENTE)* y usted (erróneamente) concluye que la variación que está probando no está funcionando de manera diferente a la original.

En los errores de tipo II, no puede ver los aumentos o las caídas reales y termina por no poder rechazar la hipótesis nula y rechazar la hipótesis alternativa.

Así es como podría cometer el error tipo II:

Volviendo al mismo sitio web B2B de arriba...

Así que supongamos que esta vez tiene la hipótesis de que agregar un descargo de responsabilidad de cumplimiento de GDPR en un lugar destacado en la parte superior de su formulario alentará a más prospectos a completarlo (lo que resultará en más clientes potenciales).

Por lo tanto, su hipótesis nula para este experimento se convierte en: El descargo de responsabilidad de cumplimiento de GDPR no afecta el llenado de formularios.

Y la hipótesis alternativa para lo mismo dice: El descargo de responsabilidad de cumplimiento de GDPR da como resultado más formularios completos.

El poder estadístico de una prueba determina qué tan bien puede detectar las diferencias en el rendimiento de sus versiones original y desafiante, en caso de que existan desviaciones. Tradicionalmente, los optimizadores intentan alcanzar el 80 % de potencia estadística porque cuanto más alta es esta métrica, menores son las posibilidades de cometer errores de tipo II.

El poder estadístico toma un valor entre 0 y 1 (ya menudo se expresa en %) y controla la probabilidad de su error tipo II (β); se calcula como: 1 – β

Cuanto mayor sea el poder estadístico de su prueba, menor será la probabilidad de encontrar errores de tipo II.

Entonces, si un experimento tiene un poder estadístico del 10%, entonces puede ser bastante susceptible a un error de tipo II. Mientras que, si un experimento tiene un poder estadístico del 80%, será mucho menos probable que cometa un error de tipo II.

Nuevamente, ejecuta su prueba, pero esta vez no nota ninguna mejora significativa en los formularios. Ambas versiones reportan conversiones casi similares. Por lo tanto, detiene su experimento y continúa con la versión original sin el descargo de responsabilidad de cumplimiento de GDPR.

Sin embargo, a medida que profundiza en los datos de sus clientes potenciales del período del experimento, descubre que, si bien la cantidad de clientes potenciales de ambas versiones (la original y la retadora) parecía idéntica, la versión GDPR le proporcionó un buen aumento significativo en el número. de clientes potenciales de Europa. (Por supuesto, podría haber utilizado la segmentación por audiencia para mostrar el experimento solo a los clientes potenciales de Europa, pero esa es otra historia).

Lo que sucedió aquí fue que terminó su prueba demasiado pronto, sin verificar si había obtenido suficiente potencia, cometiendo un error de tipo II.

Evitar errores de tipo II en sus experimentos

Para evitar errores de tipo II, ejecute pruebas con alto poder estadístico. Intente configurar sus experimentos para que pueda alcanzar al menos el 80 % de la potencia estadística. Este es un nivel aceptable de potencia estadística para la mayoría de los experimentos de optimización. Con él, puedes asegurarte de que en el 80% de los casos, al menos, rechazarás correctamente una hipótesis nula falsa.

Para hacer esto, debe observar los factores que se suman.

El mayor de ellos es el tamaño de la muestra (dado un tamaño del efecto observado). El tamaño de la muestra se relaciona directamente con el poder de una prueba. Un tamaño de muestra enorme significa una prueba de alta potencia. Las pruebas con poca potencia son muy vulnerables a los errores de tipo II, ya que sus posibilidades de detectar diferencias en los resultados de su retador y las versiones originales se reducen considerablemente, especialmente para MEI bajos (más sobre esto a continuación). Entonces, para evitar errores de tipo II, espere a que la prueba acumule suficiente potencia para minimizar los errores de tipo II. Idealmente, para la mayoría de los casos, desearía alcanzar una potencia de al menos el 80 %.

Otro factor es el efecto mínimo de interés (MEI) al que apunta para su experimento. MEI (también llamado MDE) es la magnitud mínima de la diferencia que le gustaría detectar en su KPI en cuestión. Si establece un MEI bajo (observando un aumento del 1,5 %, por ejemplo), sus posibilidades de encontrar el error de tipo II aumentan porque la detección de pequeñas diferencias necesita tamaños de muestra sustancialmente más grandes (para lograr suficiente potencia).

Y finalmente, es importante notar que tiende a haber una relación inversa entre la probabilidad de cometer un error tipo I (α) y la probabilidad de cometer un error tipo II (β). Por ejemplo, si disminuye el valor de α para reducir la probabilidad de cometer un error de tipo I (digamos que establece α en 1 %, lo que significa un nivel de confianza del 99 %), el poder estadístico de su experimento (o su capacidad, β , de detectar una diferencia cuando existe) termina reduciéndose también, aumentando así su probabilidad de obtener un error de tipo II.

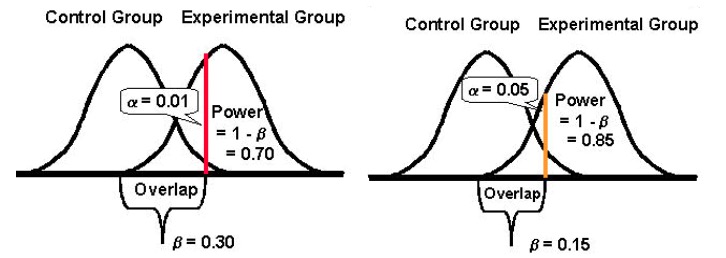
Ser más tolerante con cualquiera de los errores: tipo I y II (y lograr un equilibrio)

Reducir la probabilidad de un tipo de error aumenta la del otro tipo (dado que todo lo demás permanece igual).

Por lo tanto, debe tomar la llamada sobre qué tipo de error podría ser más tolerante.

Cometer un error tipo I, por un lado, e implementar un cambio para todos sus usuarios podría costarle conversiones e ingresos; peor aún, podría ser un asesino de conversiones también.

Por otro lado, cometer un error de tipo II y no implementar una versión ganadora para todos sus usuarios podría, nuevamente, costarle las conversiones que de otro modo podría haber ganado.

Invariablemente, ambos errores tienen un costo.

Sin embargo, dependiendo de su experimento, uno podría ser más aceptable para usted que el otro. En general, los probadores encuentran el error de tipo I unas cuatro veces más grave que el error de tipo II .

Si desea adoptar un enfoque más equilibrado, el estadístico Jacob Cohen sugiere que debe optar por un poder estadístico del 80% que viene con " un equilibrio razonable entre el riesgo alfa y beta". ” (80% de potencia también es el estándar para la mayoría de las herramientas de prueba).

Y en lo que se refiere a la significación estadística, el estándar se establece en el 95%.

Básicamente, se trata de compromiso y el nivel de riesgo que está dispuesto a tolerar. Si realmente quisiera minimizar las posibilidades de ambos errores, podría optar por un nivel de confianza del 99 % y una potencia del 99 %. Pero eso significaría que estaría trabajando con tamaños de muestra increíblemente grandes durante períodos que parecen eternamente largos. Además, incluso entonces estarías dejando margen para los errores.

De vez en cuando, concluirás un experimento de manera incorrecta. Pero eso es parte del proceso de prueba: lleva un tiempo dominar las estadísticas de prueba A/B. Investigar y volver a probar o hacer un seguimiento de sus experimentos exitosos o fallidos es una forma de reafirmar sus hallazgos o descubrir que cometió un error.