Red neuronal de una sola neurona en Python: con intuición matemática

Construyamos una red simple, muy, muy simple, pero una red completa, con una sola capa. Solo una entrada, y una neurona (que también es la salida), un peso, un sesgo.

Ejecutemos primero el código y luego analicemos parte por parte

Clone el proyecto Github, o simplemente ejecute el siguiente código en su IDE favorito.

Si necesita ayuda para configurar un IDE, describí el proceso aquí.

Si todo va bien, obtendrá este resultado:

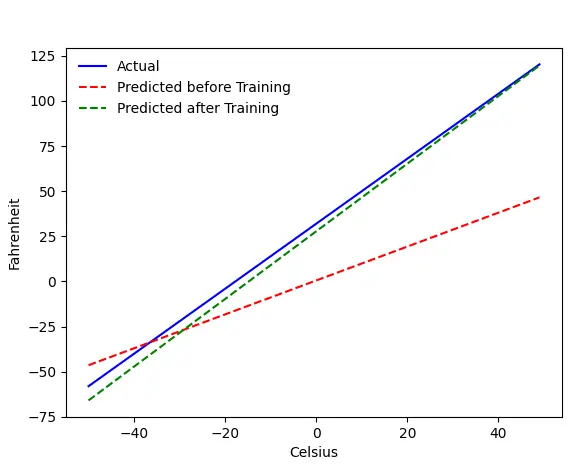
El problema: Fahrenheit a partir de Celsius

Entrenaremos a nuestra máquina para predecir Fahrenheit a partir de Celsius. Como puede comprender por el código (o el gráfico), la línea azul es la relación Celsius-Fahrenheit real. La línea roja es la relación predicha por nuestra máquina de bebés sin ningún entrenamiento. Finalmente, entrenamos la máquina, y la línea verde es la predicción después del entrenamiento.

Mire las líneas #65–67: antes y después del entrenamiento, está prediciendo usando la misma función ( get_predicted_fahrenheit_values() ). Entonces, ¿qué está haciendo el tren mágico ()? Vamos a averiguar.

Estructura de red

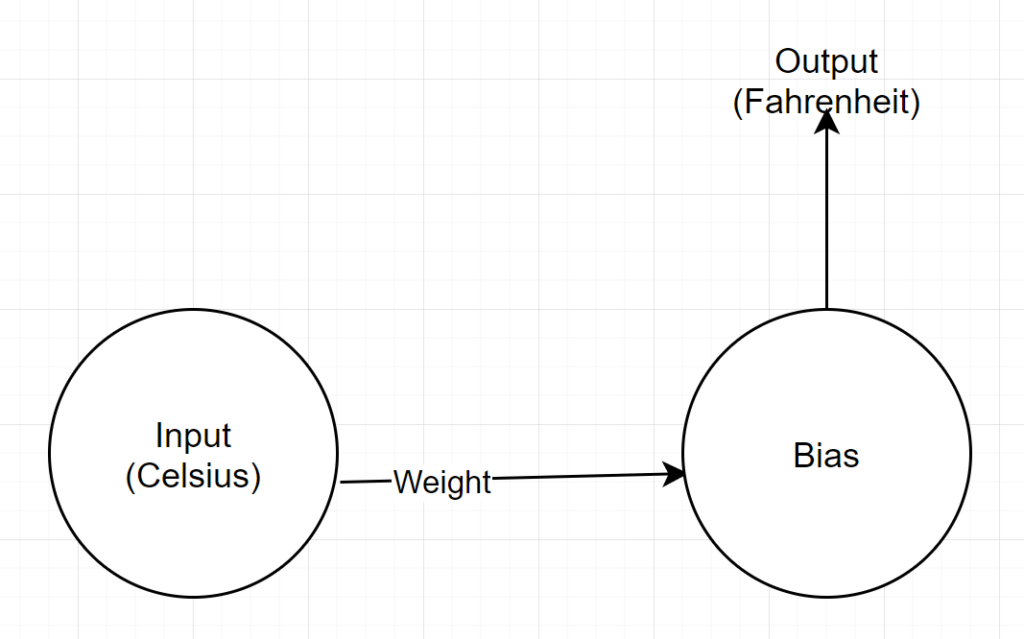
Entrada: un número que representa Celsius

Peso: un flotador que representa el peso

Sesgo: un flotador que representa el sesgo

Salida: Un flotador que representa el Fahrenheit predicho

Entonces, tenemos un total de 2 parámetros: 1 peso y 1 sesgo

Análisis de código

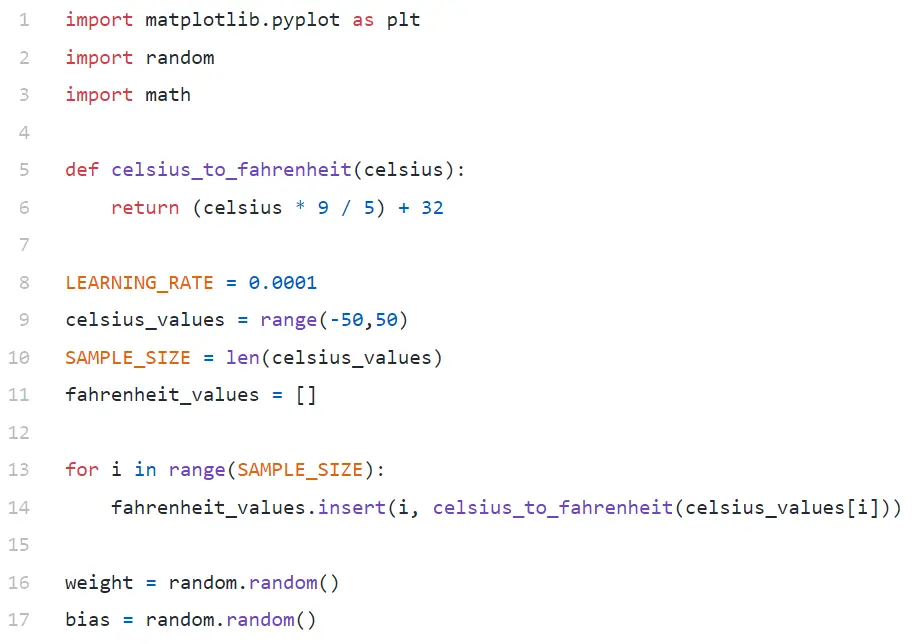
En Line#9, estamos generando una matriz de 100 números entre -50 y +50 (excluyendo 50, la función de rango excluye el valor del límite superior).

En la Línea #11–14, estamos generando los grados Fahrenheit para cada valor Celsius.

En las líneas n.° 16 y n.° 17, estamos inicializando el peso y el sesgo.

tren()

Estamos ejecutando 10000 iteraciones de entrenamiento aquí. Cada iteración está hecha de:

1. adelante (línea #57) pase
2. pase hacia atrás (línea 58)
3. update_parameters (Línea#59)

Si es nuevo en python, puede parecerle un poco extraño: las funciones de python pueden devolver múltiples valores como tupla .

Note que update_parameters es lo único que nos interesa. Todo lo demás que estamos haciendo aquí es evaluar los parámetros de esta función, que son los gradientes (a continuación explicaremos qué son los gradientes) de nuestro peso y sesgo.

1. grad_weight: un flotante que representa el gradiente de peso
2. grad_bias: un flotante que representa el gradiente de sesgo

Obtenemos estos valores llamando hacia atrás, pero requiere salida, que obtenemos llamando hacia adelante en la línea #57.

delantero()

Tenga en cuenta que aquí celsius_values ​​y fahrenheit_values ​​son matrices de 100 filas:

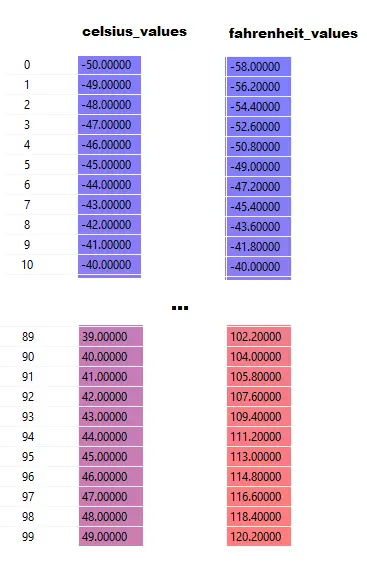
Después de ejecutar Line#20–23, para un valor Celsius, digamos 42

salida = 42 * peso + sesgo

Entonces, para 100 elementos en celsius_values ​​, la salida será una matriz de 100 elementos para cada valor celsius correspondiente.

Las líneas n.º 25 a 30 calculan la pérdida mediante la función de pérdida del error cuadrático medio (MSE), que es solo un nombre elegante del cuadrado de todas las diferencias dividido por el número de muestras (100 en este caso).

Una pequeña pérdida significa una mejor predicción. Si continúa imprimiendo la pérdida en cada iteración, verá que está disminuyendo a medida que avanza el entrenamiento.

Finalmente, en la línea n.º 31 estamos devolviendo la producción y la pérdida previstas.

hacia atrás

Solo estamos interesados ​​en actualizar nuestro peso y sesgo. Para actualizar esos valores, tenemos que conocer sus gradientes, y eso es lo que estamos calculando aquí.

Observe que los gradientes se calculan en orden inverso. Primero se calcula el gradiente de salida, y luego el peso y el sesgo, por lo que el nombre "propagación hacia atrás". La razón es que, para calcular el gradiente de peso y sesgo, necesitamos conocer el gradiente de salida, para poder usarlo en la fórmula de la regla de la cadena .

Ahora echemos un vistazo a lo que son las reglas del gradiente y de la cadena.

Degradado

En aras de la simplicidad, considere que solo tenemos un valor de valores_celsius y valores_fahrenheit , 42 y 107.6 respectivamente.

Ahora, el desglose del cálculo en la línea 30 se convierte en:

pérdida = (107.6 — (42 * peso + sesgo))² / 1

Como puede ver, la pérdida depende de 2 parámetros: pesos y sesgo. Considere el peso. Imagínese, lo inicializamos con un valor aleatorio, digamos, 0,8, y después de evaluar la ecuación anterior, obtenemos 123,45 como valor de pérdida . En función de este valor de pérdida, debe decidir cómo actualizará el peso. ¿Deberías hacerlo 0.9 o 0.7?

Debe actualizar el peso de manera que en la próxima iteración obtenga un valor más bajo para la pérdida (recuerde, el objetivo final es minimizar la pérdida). Entonces, si el aumento de peso aumenta la pérdida, la disminuiremos. Y si el aumento de peso disminuye la pérdida, la aumentaremos.

Ahora, la pregunta, ¿cómo sabemos si el aumento de peso aumentará o disminuirá la pérdida? Aquí es donde entra el gradiente . En términos generales, el gradiente se define por la derivada. Recuerde de su cálculo de la escuela secundaria, ∂y/∂x (que es derivada parcial/gradiente de y con respecto a x) indica cómo cambiará y con un pequeño cambio en x.

Si ∂y/∂x es positivo, significa que un pequeño incremento en x aumentará y.

Si ∂y/∂x es negativo, significa que un pequeño incremento en x disminuirá y.

Si ∂y/∂x es grande, un pequeño cambio en x provocará un gran cambio en y.

Si ∂y/∂x es pequeño, un pequeño cambio en x provocará un pequeño cambio en y.

Entonces, de los gradientes, obtenemos 2 información. En qué dirección se debe actualizar el parámetro (aumento o disminución) y cuánto (grande o pequeño).

Cadena de reglas

Informalmente hablando, la regla de la cadena dice:

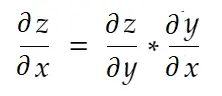
Considere el ejemplo de peso anterior. Necesitamos calcular grad_weight para actualizar este peso, que será calculado por:

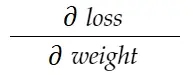
Con la fórmula de la regla de la cadena, podemos derivarla:

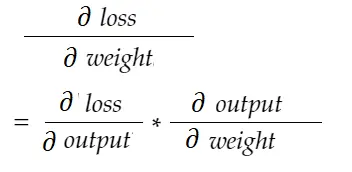
Del mismo modo, gradiente de sesgo:

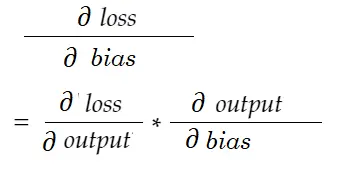
Dibujemos un diagrama de dependencia.

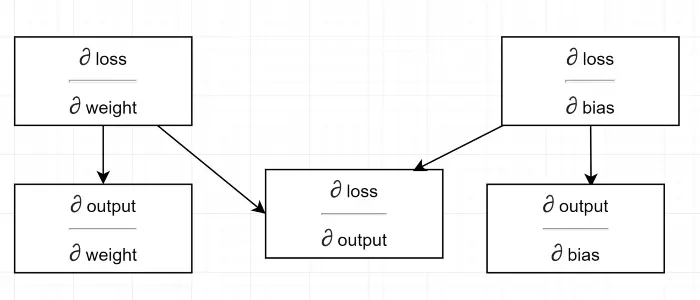
Ver que todos los cálculos dependen del gradiente de salida (∂ pérdida/∂ salida) . Es por eso que lo estamos calculando primero en el paso de regreso (Líneas #34–36).

De hecho, en marcos de ML de alto nivel, por ejemplo en PyTorch, ¡no tiene que escribir códigos para backpass! Durante el paso hacia adelante, crea gráficos computacionales, y durante el paso hacia atrás, pasa por la dirección opuesta en el gráfico y calcula los gradientes utilizando la regla de la cadena.

∂ pérdida / ∂ salida

Definimos esta variable por grad_output en el código, que calculamos en la línea 34–36. Averigüemos la razón detrás de la fórmula que usamos en el código.

Recuerde, estamos alimentando los 100 valores_celsius en la máquina juntos. Entonces, grad_output será una matriz de 100 elementos, cada elemento conteniendo un gradiente de salida para el elemento correspondiente en celsius_values . Para simplificar, consideremos que solo hay 2 elementos en celsius_values .

Entonces, desglosando la línea #30,

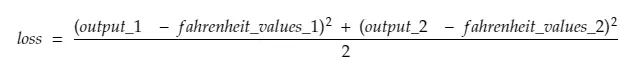
donde,

salida_1 = valor de salida para el primer valor Celsius

output_2 = valor de salida para el segundo valor Celsius

fahreinheit_values_1 = Valor real en grados Fahreinheit para el primer valor Celsius

fahreinheit_values_1 = Valor real en grados Fahreinheit para el segundo valor Celsius

Ahora, la variable resultante grad_output contendrá 2 valores: gradiente de output_1 y output_2, lo que significa:

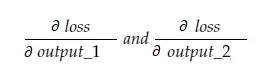
Calculemos solo el gradiente de salida_1, y luego podemos aplicar la misma regla para los demás.

¡Tiempo de cálculo!

Que es lo mismo que la línea #34-36.

gradiente de peso

Imagínese, solo tenemos un elemento en celsius_values. Ahora:

Que es lo mismo que la Línea #38–40. Para 100 valores_celsius, se sumarán los valores de gradiente para cada uno de los valores. Una pregunta obvia sería por qué no estamos reduciendo el resultado (es decir, dividiendo con SAMPLE_SIZE). Dado que estamos multiplicando todos los gradientes con un factor pequeño antes de actualizar los parámetros, no es necesario (consulte la última sección Actualización de parámetros).

Gradiente de sesgo

Que es lo mismo que la Línea #42. Al igual que los gradientes de peso, estos valores para cada una de las 100 entradas se resumen. Nuevamente, está bien ya que los gradientes se multiplican con un factor pequeño antes de actualizar los parámetros.

Actualización de parámetros

Finalmente, estamos actualizando los parámetros. Tenga en cuenta que los gradientes se multiplican por un factor pequeño (LEARNING_RATE) antes de restarlos, para que el entrenamiento sea estable. Un valor alto de LEARNING_RATE causará un problema de exceso y un valor extremadamente pequeño hará que el entrenamiento sea más lento, lo que podría necesitar muchas más iteraciones. Deberíamos encontrar un valor óptimo para él con algo de prueba y error. Hay muchos recursos en línea, incluido este para obtener más información sobre el ritmo de aprendizaje.

Tenga en cuenta que la cantidad exacta que ajustamos no es extremadamente crítica. Por ejemplo, si ajusta LEARNING_RATE un poco, las variables descent_grad_weight y descent_grad_bias (Line#49–50) cambiarán, pero es posible que la máquina siga funcionando. Lo importante es asegurarse de que estas cantidades se obtengan reduciendo los gradientes con el mismo factor (tasa de aprendizaje en este caso). En otras palabras, “mantener proporcional el descenso de las pendientes” importa más que “cuánto descienden ”.

Observe también que estos valores de gradiente son en realidad la suma de los gradientes evaluados para cada una de las 100 entradas. Pero dado que estos se escalan con el mismo valor, está bien como se mencionó anteriormente.

Para actualizar los parámetros, debemos declararlos con la palabra clave global (en la línea 47).

A dónde ir desde aquí

El código sería mucho más pequeño al reemplazar los bucles for con comprensión de lista en forma pythonic. Échale un vistazo ahora, no te llevará más de unos minutos entenderlo.

Si entendió todo hasta ahora, probablemente sea un buen momento para ver las partes internas de una red simple con múltiples neuronas/capas. Aquí hay un artículo.