Distribución normal: una introducción intuitiva sin matemáticas

Trataré de mantener este artículo libre de ecuaciones y jerga en la boca, tanto como sea posible. Sin embargo, necesito que al menos tengas las siguientes capacidades:

• Capaz de interpretar gráficos simples.
• Conocimientos de nivel elemental en probabilidad. Al menos entiendes que hay un 50% de probabilidad de que salga cara si tiro una moneda.
• Cálculo integral y física cuántica (¡es broma!)

Por qué distribución normal

Una forma intuitiva de entender algo es investigar por qué es necesario. Hagámoslo para la distribución normal (también llamada Distribución Gaussiana).

Digamos que tienes un hábito divertido. Todos los días lanzas una moneda 100 veces. Es "normal" esperar que tenga cabeza 50 veces, o cerca de 50 veces la mayor parte del día. En raras ocasiones, hay buenos días para la cabeza: puede obtener alrededor de 55 veces y muy raramente más de 65 veces.

Ahora, desea cuantificar esta "rareza". Entonces, comienzas a llevar un registro de cuántas veces tienes la cabeza todos los días.

Número de cabezas cada día en un año

A continuación se muestran los datos después de un año (365 días): el primero es el número de cabezas que obtuvo el primer día y el último es el número de cabezas que obtuvo el último día. No es necesario que verifique todos los números a continuación, pero es fácil darse cuenta de que la mayoría de ellos rondan los 50.

56, 47, 54, 50, 57, 51, 57, 48, 54, 62, 42, 51, 37, 42, 50, 37, 59, 48, 46, 51, 61, 47, 46, 48, 63, 55, 50, 50, 43, 46, 56, 49, 50, 54, 52, 47, 51, 59, 61, 53, 44, 53, 59, 58, 54, 54, 50, 49, 51, 46, 43, 51, 49, 54, 46, 44, 41, 51, 51, 49, 64, 46, 46, 46, 52, 48, 57, 49, 42, 46, 55, 50, 52, 51, 47, 53, 50, 48, 58, 43, 60, 49, 46, 42, 53, 45, 57, 48, 52, 47, 47, 47, 42, 57, 60, 49, 48, 50, 51, 47, 48, 52, 47, 45, 51, 55, 51, 45, 46, 46, 40, 52, 57, 48, 51, 48, 44, 46, 41, 59, 60, 46, 44, 36, 48, 52, 49, 49, 49, 51, 41, 49, 51, 51, 42, 51, 45, 54, 50, 48, 49, 43, 52, 53, 52, 53, 48, 37, 53, 54, 41, 48, 52, 46, 47, 57, 50, 49, 46, 57, 67, 50, 54, 48, 50, 60, 43, 49, 57, 57, 45, 55, 57, 52, 46, 48, 49, 51, 45, 48, 44, 48, 55, 51, 59, 52, 50, 55, 51, 46, 48, 51, 46, 50, 49, 50, 47, 51, 43, 46, 48, 56, 47, 57, 44, 54, 52, 55, 46, 49, 53, 40, 54, 54, 49, 50, 53, 41, 55, 50, 42, 58, 47, 53, 55, 45, 52, 61, 50, 49, 48, 51, 50, 56, 44, 47, 45, 48, 63, 43, 52, 55, 46, 48, 52, 49, 56, 62, 57, 54, 47, 51, 52, 43, 45, 57, 51, 46, 42, 52, 57, 54, 48, 54, 51, 49, 51, 42, 52, 50, 52, 61, 61, 44, 45, 48, 49, 48, 46, 47, 57, 44, 44, 47, 52, 47, 42, 48, 51, 58, 36, 57, 53, 49, 52, 50, 52, 56, 44, 56, 46, 42, 46, 43, 56, 49, 44, 38, 46, 52, 49, 58, 51, 49, 48, 52, 57, 43, 48, 40, 52, 54, 40, 54, 45, 49, 41, 57, 50, 52, 43, 54, 49, 45, 44, 53, 49, 43, 51, 50, 56, 45, 46, 47, 41, 52, 59, 52, 50, 48, 58, 52, 51, 55, 49, 41, 38, 57, 56, 41, 54, 44, 47, 60, 44

Visualice mejor con histograma

Tracemos un histograma a partir de los datos anteriores:

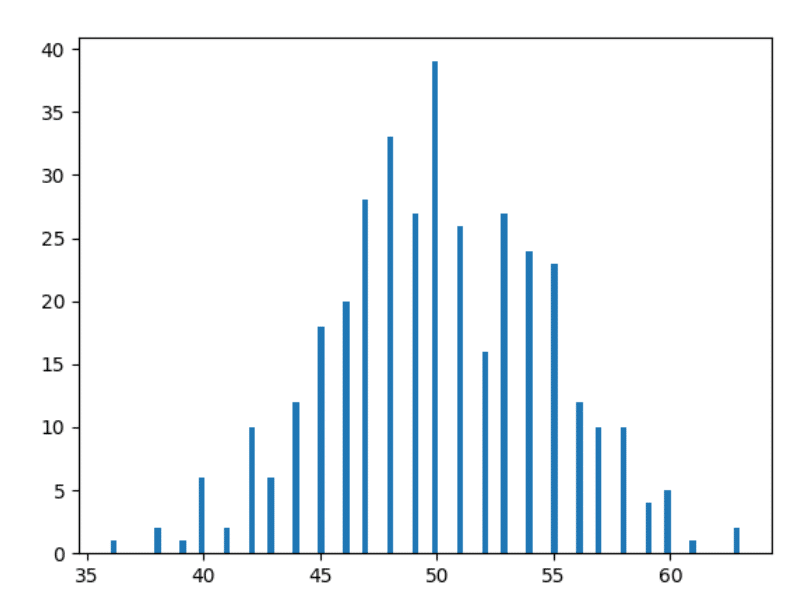
¡Ajá! ¿No se parece ya a la imagen que ha estado viendo en Internet cuando ha estado buscando en Google "Distribución normal"? ¡Estamos casi alli!

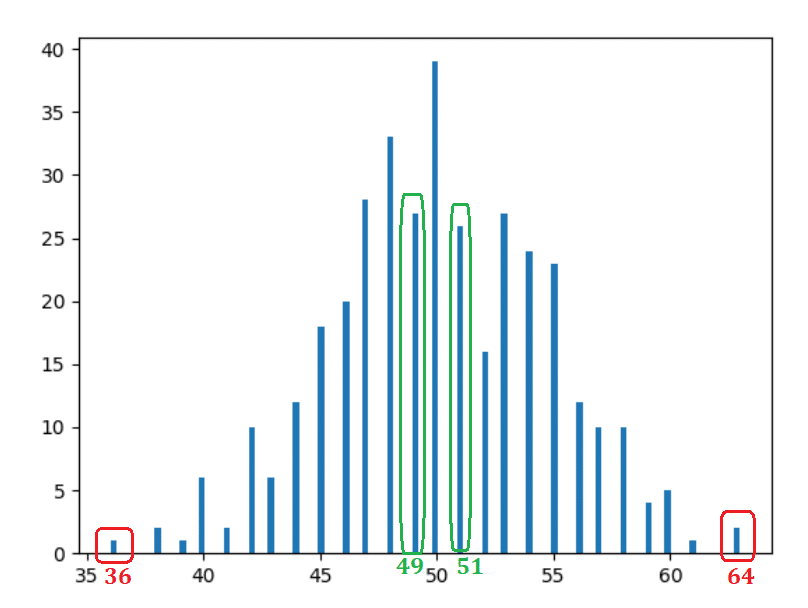
Entonces, si no entiende los histogramas, acabamos de trazar aquí el número de días que obtuvimos un recuento particular para la cabeza. Por ejemplo, obtuvimos cabeza 36 veces en 2 días particulares del año (verifique los datos de arriba si no me cree), es por eso que hay una barra de 2 unidades de altura en el punto horizontal en 36 (el rojo rectángulo a la izquierda en la imagen de abajo).

Observaciones

1. Bastante obvio y esperado: 50 cabezas ocurrieron la mayoría de las veces.
2. Cuanto más nos alejamos del centro (50), la ocurrencia es mayormente decreciente.
3. Las barras a la misma distancia toman formas similares. Por ejemplo, si mueve una unidad hacia la izquierda (49) o hacia la derecha (51), las ocurrencias son similares: 30 y 31 respectivamente (los rectángulos verdes). Si te mueves 14 unidades hacia la izquierda (36) o hacia la derecha (64), las ocurrencias vuelven a ser similares: 2 y 1 respectivamente (rectángulos rojos).

datos de 10 años

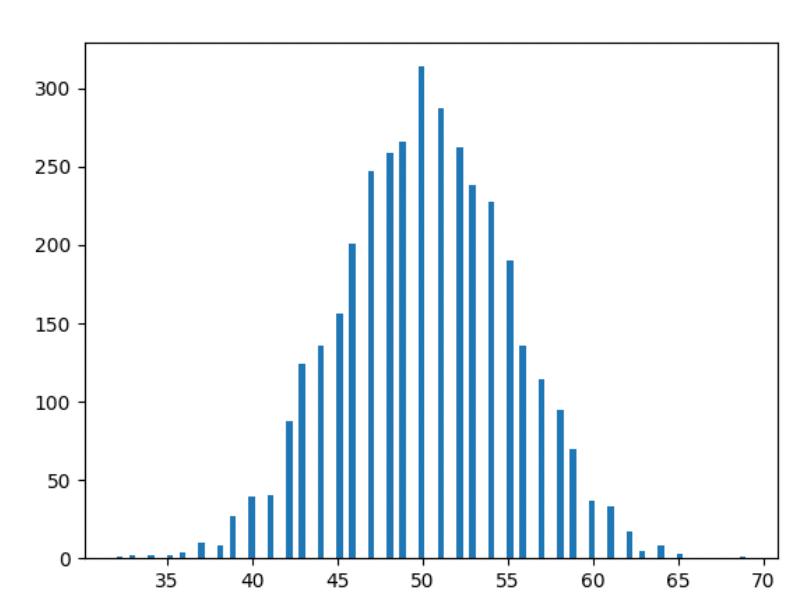
Ahora avancemos un poco y tracemos los datos de 10 años.

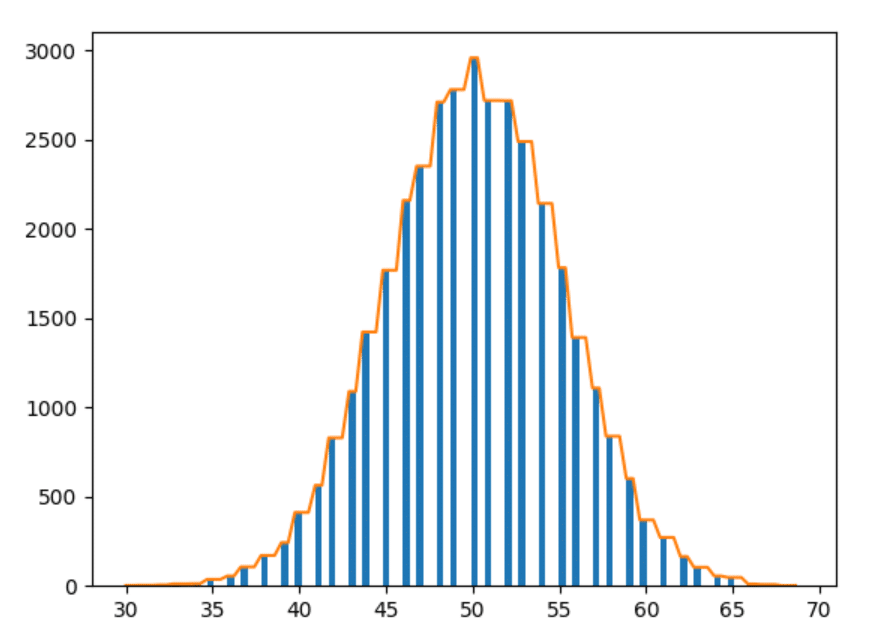
datos de 1000 años

Bien, el último. Grafiquemos los datos de 1000 años.

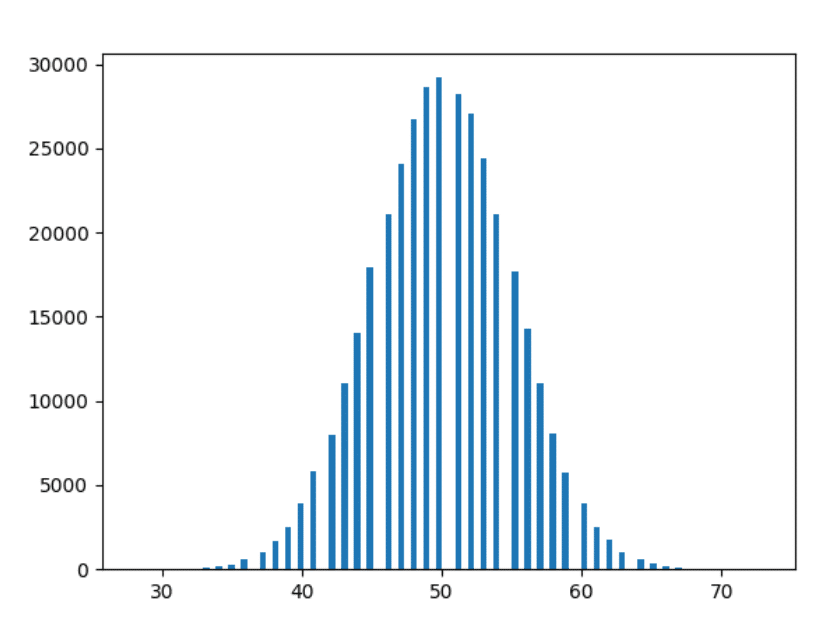
Observaciones

1. Cuanto más experimentamos, más suaves son las formas.
2. Cuanto más experimentamos, más las barras siguen las observaciones anteriores (es decir, las barras a una distancia similar toman formas más cercanas).

¿Dónde está la maldita distribución normal?

De acuerdo, demasiado trasfondo, ahora vayamos al grano.

Veamos la respuesta sugerida por Google:

Algunas cosas en esta definición:

Variable aleatoria: En pocas palabras, una variable aleatoria es un conjunto de valores posibles de un experimento aleatorio como el lanzamiento de una moneda. En nuestro ejemplo, el posible valor de nuestro experimento es Cara o Cruz .

En forma de campana: ¿Te diste cuenta de que nuestro histograma está tomando forma de campana?

Simétrico: las barras a la misma distancia tienen formas similares, ¿no es simétrico?

Entonces, la distribución normal representa la distribución de resultados para eventos como el lanzamiento de una moneda, donde la distribución tiende a mantener algunas propiedades, incluida la simetría y la forma de campana.

¿Qué fenómenos además del lanzamiento de una moneda siguen una distribución normal?

Algunos ejemplos geniales aquí.

• Altura en la población: más personas caen en el grupo de altura promedio. Es raro encontrar personas extremadamente altas o extremadamente bajas. Y las posibilidades de encontrar extremadamente alto y extremadamente bajo son casi iguales.
• tirar un dado
• Tamaño del zapato
• CI
• Y muchas otras…

¿Siguen estos fenómenos estrictamente una distribución normal?

La respuesta simple es no. Aunque, como vimos anteriormente, cuanto más experimente, más seguirán los datos las propiedades de distribución normales. Pero no hay garantía de que algún evento improbable no ocurra de todos modos.

¿Todas las distribuciones de probabilidad en el universo son distribución normal?

No. Hay muchos fenómenos que están determinados por algún otro tipo de distribución.

• La probabilidad de que llegue un número dado de clientes, llamadas telefónicas, accidentes, eventos deportivos e inundaciones siguen la distribución de Poisson .
• Para las ventas comerciales, el 20% de los clientes de una empresa son responsables del 80% de las ventas. ( Distribución de Pareto )
• Patrones de tráfico en una ciudad — Distribución Exponencial
• Selección aleatoria de miembros para un equipo de una población de niñas y niños — Distribución Hipergeométrica

Y muchos más …

Produje la lista anterior simplemente buscando en Google "ejemplo de la vida real" con algunas distribuciones enumeradas aquí, no es que las entienda todas. 😉

¿Hay alguna razón por la que algunos fenómenos naturales tiendan a seguir una distribución normal?

Sí, citando mi explicación favorita:

La explicación habitual viene dada por otro nombre para la distribución normal, que es la "distribución de error". La idea es que los errores son generalmente aleatorios, por lo que es probable que vayan en una dirección o en la otra. Por ejemplo, es probable que el tirador dispare un poco a la izquierda, un poco a la derecha, o un poco alto que un poco bajo. Por lo tanto, un gráfico de qué tan lejos están los tiros de la diana reflejará esta tendencia aleatoria y será simétrico alrededor de la media. De manera similar, con la altura y la inteligencia, muchos genes (quizás miles) contribuyen a estos resultados, al igual que una gran cantidad de factores ambientales, como la nutrición, las enfermedades, los bajos ingresos, etc.

Parámetros de la distribución normal

Si tiene una intuición de la discusión hasta ahora, ya es el ganador. Misión cumplida. El resto del artículo es un bono.

Todos los gráficos de distribución normal que ves tienen formas diferentes. Algunos de ellos son más planos que otros. Algunos de ellos tienen buenas alturas. Todas estas formas están controladas por solo 2 parámetros:

Significar

La media se define por el promedio. Define la altura de la campana. Para el ejemplo del lanzamiento de una moneda, la media está cerca de 50, que es la ubicación superior en el gráfico.

Desviación Estándar

Dado que prometo que este artículo estará libre de ecuaciones, no estoy dando su representación matemática aquí. Pero no es tan difícil de todos modos. La desviación estándar es una métrica para representar la diversidad de los datos.

Por ejemplo, la desviación estándar de la edad en el cuidado de los niños será menor que la desviación estándar de la edad en el club de aficionados al fútbol, ​​ya que la diferencia de edad entre el grupo más joven y el de mayor edad debería ser mucho mayor en el club de aficionados al fútbol.

La desviación estándar determina el ancho de la curva. Una desviación estándar pequeña produce una curva pronunciada y una desviación estándar mayor produce una curva más plana.