Estadísticas bayesianas: un manual básico rápido y sin exageraciones para un probador A/B
Publicado: 2022-06-23
¿Qué tan seguro está de su capacidad para interpretar los resultados proporcionados por su herramienta de prueba A/B?
Supongamos que está utilizando una herramienta basada en estadísticas bayesianas y le dice que "B" tiene un 70 % de posibilidades de vencer a "A", por lo que "B" es el ganador. ¿Sabe lo que eso significa y cómo debería informar su estrategia de CRO?
En este artículo, aprenderá los fundamentos de las estadísticas bayesianas que lo ayudarán a recuperar el control de sus pruebas A/B, incluido
- Una visión imparcial de las estadísticas bayesianas
- Ventajas y desventajas frecuentista vs bayesiana
- La preparación que necesita para interpretar y utilizar con confianza los resultados de las pruebas Bayesianas A/B mientras evita algunas trampas de mitos comunes.
- ¿Qué es la estadística bayesiana?
- La historia del origen bayesiano
- Un ejemplo de estadística bayesiana aplicada a las pruebas A/B
- Un breve glosario de términos bayesianos importantes para los probadores A/B
- Inferencia bayesiana
- La probabilidad condicional
- Distribución de probabilidad/Distribución de verosimilitud
- Distribución de creencias previas
- Conjugación
- Prioridades Conjugadas
- Función de pérdida
- ¿Qué es la estadística frecuentista?
- Pruebas A/B Bayesianas vs Frecuentes
- El marco frecuentista
- El Marco Bayesiano
- ¿Qué le dicen realmente las estadísticas bayesianas en las pruebas A/B?
- Probabilidad de ser el mejor (P2BB)
- Aumento esperado
- Pérdida esperada
- Mitos sobre las estadísticas bayesianas que se deben evitar
- Mito n.º 1: los bayesianos afirman sus suposiciones, los frecuentistas no
- Mito #2. Los métodos bayesianos le brindan las respuestas que realmente desea
- Mito n.° 3: la inferencia bayesiana lo ayuda a comunicar la incertidumbre mejor que la inferencia frecuentista
- Mito #4. Los resultados de las pruebas Bayesianas A/B son inmunes a las miradas a escondidas
- Mito #5. Las estadísticas frecuentistas son ineficientes ya que debe esperar un tamaño de muestra fijo
- Entonces, ¿debería elegir bayesiano o frecuentista? Hay un Lugar para Ambos.
- Punto clave
¿Listo? Empecemos con lo básico.
¿Qué es la estadística bayesiana?
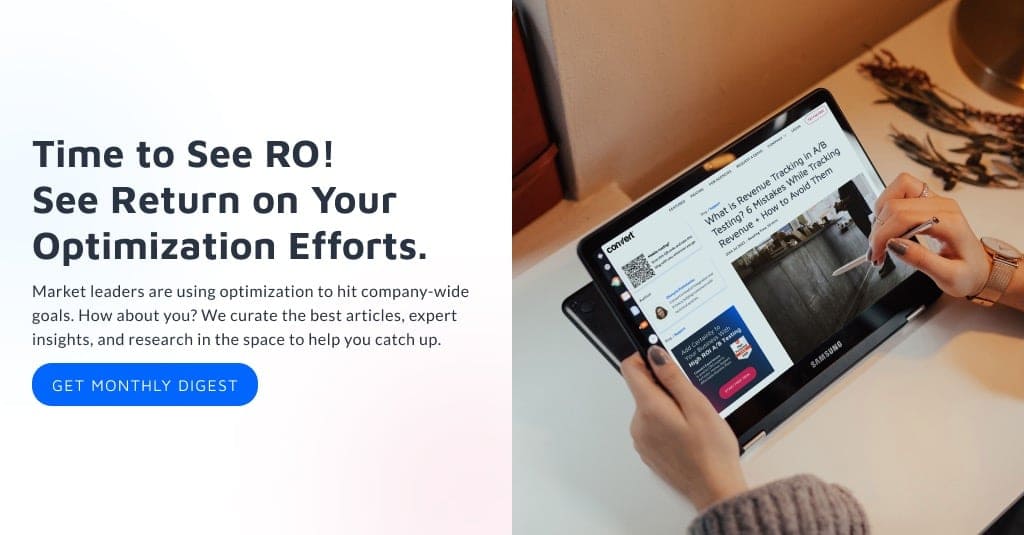
La estadística bayesiana es un enfoque del análisis estadístico que se basa en el teorema de Bayes, que actualiza las creencias sobre los eventos a medida que se recopilan nuevos datos o pruebas sobre esos eventos. Aquí, la probabilidad es una medida de la creencia de que ocurre un evento.
Lo que esto significa: si tiene una creencia previa sobre un evento y obtiene más información relacionada con él, esa creencia cambiará (o al menos se ajustará) a una creencia posterior .
Esto es útil para comprender la incertidumbre o cuando se trabaja con muchos datos ruidosos, como en la optimización de la tasa de conversión para el comercio electrónico y el aprendizaje automático.
Imaginemos esto:
Digamos, por ejemplo, que está viendo una carrera de carritos de supermercado en la universidad y luego un espectador emocionado lo desafía a una apuesta de que el tipo de la camiseta roja que lleva a la dama de la camiseta verde ganará. Lo piensas y respondes que el chico de la chaqueta negra y la chica con capucha negra ganarán en su lugar.

Otro espectador sobre tu cabeza y te susurró un consejo: "El chico de la camiseta roja ganó las últimas 3 carreras de 4". ¿Qué pasa con tu apuesta? Ya no estás muy seguro, ¿verdad?
Supongamos que también supieras que la última vez que el chico de la chaqueta negra usó sus gafas de sol de la suerte, ganó. Y las veces que no la usó, ganó el de la camiseta roja.
Hoy ves que el chico de la chaqueta negra lleva esas gafas. Su creencia cambia de nuevo. Ahora tienes más fe en tu apuesta, ¿correcto? En esta historia, actualizaste tu creencia cada vez que obtuviste evidencia de nuevos datos. Ese es el enfoque bayesiano.
La historia del origen bayesiano
Cuando el reverendo Thomas Bayes pensó por primera vez en su teoría, no pensó que mereciera la pena publicarla. Entonces, permaneció en sus notas durante más de una década. Fue cuando su familia le pidió a Richard Price que revisara sus notas que Price descubrió las notas que formaban la base del Teorema de Bayes.
Comenzó con un experimento mental para Bayes. Pensó en sentarse de espaldas a una mesa perfectamente plana y cuadrada y pedirle a un asistente que arrojara una pelota sobre la mesa.
La pelota podría caer en cualquier parte de la mesa, pero Bayes pensó que podía adivinar dónde actualizando sus conjeturas con nueva información. Cuando la pelota caía sobre la mesa, le pedía al asistente que le dijera si caía a la izquierda o a la derecha, delante o detrás de donde había caído la bola anterior.
Lo notó y escuchó mientras caían más bolas sobre la mesa. Con información adicional como esta, descubrió que podía mejorar la precisión de sus conjeturas con cada lanzamiento. Esto trajo la idea de actualizar nuestra comprensión a medida que adquiríamos más evidencia de la observación.
El enfoque bayesiano para el análisis de datos se aplica en varios campos, como la ciencia y la ingeniería, e incluso incluye deportes y leyes.
En experimentos controlados aleatorios en línea, específicamente pruebas A/B, puede utilizar el enfoque bayesiano en 4 pasos:
- Identifique su distribución anterior.
- Elija un modelo estadístico que refleje sus creencias.
- Ejecute el experimento.
- Después de la observación, actualice sus creencias y calcule una distribución posterior.
Actualizas tus creencias usando un conjunto de reglas llamado algoritmo bayesiano.
Un ejemplo de estadística bayesiana aplicada a las pruebas A/B
Ilustremos un ejemplo de prueba Bayesiana A/B.
Imagina que realizamos una prueba A/B simple en el botón CTA de una tienda Shopify. Para "A", usamos "Agregar al carrito" y para "B", usamos "Agregar a su carrito".
Así es como un frecuentador abordará la prueba.
Hay dos mundos alternativos: uno en el que A y B no son diferentes, por lo que la prueba no mostrará ninguna diferencia en la tasa de conversión. Esa es la hipótesis nula. Y en el otro mundo, hay una diferencia, por lo que un botón funcionará mejor que el otro.
El frecuentador asumirá que vivimos en el mundo 1 donde no hay diferencia en los botones de CTA, es decir, suponiendo que la hipótesis nula sea cierta. Y luego intentarán probar que eso es incorrecto a un nivel predeterminado de certeza llamado nivel de significación.
Pero así es como un bayesiano abordará la misma prueba:
Comienzan con la creencia previa de que los botones A y B tienen las mismas posibilidades de producir una tasa de conversión entre 0 y 100%. Por lo tanto, hay igualdad de botones desde el principio: ambos tienen un 50% de posibilidades de ser los mejores.
Luego comienza la prueba y se recopilan los datos. A partir de la observación de nueva información, los probadores bayesianos A/B actualizarán sus conocimientos. Entonces, si B se muestra prometedor, pueden llegar a una creencia posterior basada en esa observación que dice: "B tiene un 61% de posibilidades de vencer a A".
Hay diferencias fundamentales entre los dos métodos.
Por eso es importante para nosotros mantener un enfoque imparcial en las pruebas Bayesianas A/B.
La mayoría de las herramientas de pruebas Bayesianas A/B, tal vez con fines de marketing, adoptan una postura anti-frecuentista extrema y promueven el argumento de que Bayesian es mejor para decirle qué variante es más "rentable".
Pero, ¿algún enfoque estadístico único para las pruebas A/B posee los derechos exclusivos de los conocimientos?
Si se lleva más allá el argumento bayesiano, es posible que se enfrenten a estudios en los que los encuestados dicen que quieren saber cuál es el mejor curso de acción o que quieren maximizar las ganancias o algo similar. Esto coloca la pregunta firmemente en el territorio de la teoría de la decisión, algo en lo que ni la inferencia bayesiana ni la inferencia frecuentista pueden tener una opinión directa.
Georgi Georgiev, creador de Analytics-toolkit.com y autor de "Métodos estadísticos en pruebas A/B en línea"
Nos sumergiremos brevemente en estos detalles en las secciones siguientes. Por ahora, hagamos que el resto de este manual sea fácil de comprender.
Un breve glosario de términos bayesianos importantes para los probadores A/B
Inferencia bayesiana
La inferencia bayesiana actualiza la probabilidad de una hipótesis con nuevos datos. Se basa en creencias y probabilidades.
La inferencia bayesiana aprovecha la probabilidad condicional para ayudarnos a comprender cómo los datos afectan nuestras creencias. Digamos que empezamos con una creencia previa de que el cielo es rojo. Después de mirar algunos datos, pronto nos daríamos cuenta de que esta creencia previa es incorrecta. Entonces, realizamos una actualización bayesiana para mejorar nuestro modelo incorrecto sobre el color del cielo, y terminamos con una creencia posterior más precisa .
Michael Berk en Hacia la ciencia de datos
La probabilidad condicional
La probabilidad condicional es la probabilidad de un evento dado que ocurrió otro evento. Es decir, la probabilidad de A bajo la condición B.
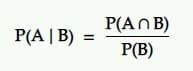
Traducción: La probabilidad de que suceda un evento A dado otro evento B es igual a la probabilidad de que B y A sucedan juntos dividida por la probabilidad del evento B.
Distribución de probabilidad/Distribución de verosimilitud
Las distribuciones de probabilidad son distribuciones que muestran la probabilidad de que sus datos asuman un valor específico.
Donde sus datos pueden asumir múltiples valores, por ejemplo, una categoría como colores que podrían ser gris, rojo, naranja, azul, etc., su distribución es multinomial. Para un conjunto de números, la distribución podría ser normal. Y para valores de datos que podrían ser sí/no o verdadero/falso, sería binomial.
Distribución de creencias previas
O la distribución de probabilidad previa, simplemente llamada previa, expresa su creencia antes de obtener evidencia de nuevos datos. Por lo tanto, es una expresión de su creencia inicial que actualizará después de considerar alguna evidencia utilizando el análisis (o inferencia) bayesiano.
Conjugación
En primer lugar, conjugado se refiere a estar unidos, generalmente en pares. En la teoría de la probabilidad bayesiana, la conjugación supone que el anterior es conjugado con la probabilidad.
Si el posterior tiene la misma forma funcional que el anterior, entonces el anterior es conjugado con la función de probabilidad. Esto muestra cómo la función de probabilidad actualiza la distribución anterior.
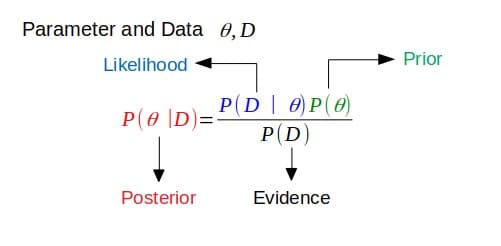
Prioridades Conjugadas
Esto está relacionado con la definición anterior. Si la posterior está en la misma familia de distribución de probabilidad (o tiene la misma forma funcional) que la distribución de probabilidad anterior, entonces la anterior y la posterior son distribuciones conjugadas. En este caso, el anterior se llama conjugado anterior para la función de verosimilitud.
Pueden ser subjetivos (basados en el conocimiento del experimentador), objetivos e informativos (basados en datos históricos) o no informativos.
Función de pérdida
Una función de pérdida es una forma de cuantificar la pérdida midiendo qué tan mala es nuestra estimación actual. Nos ayuda a minimizar la pérdida para la prueba de hipótesis, especialmente al expresar una inferencia que se encuentra en un rango de valores probables, y respalda la toma de decisiones con los resultados de nuestra prueba.
Ahora que está fuera del camino, podemos seguir adelante.
Si ha estado dando vueltas por el bloque por un tiempo, probablemente se haya encontrado con más de unos pocos memes de estadísticas Frequentist vs Bayesian.

Ambos lados parecen buscar respuestas en direcciones opuestas, pero ¿es realmente así? Para entender esto mejor (sin dejar de ser imparcial), visitemos el campo de Frequentists.
¿Qué es la estadística frecuentista?
Esta es la primera técnica inferencial que la mayoría de la gente aprende en estadística. Las estadísticas frecuentistas calculan la probabilidad de que un evento (hipótesis) ocurra con frecuencia bajo las mismas condiciones.
La prueba de hipótesis A/B utilizando el enfoque frecuentista sigue estos pasos:
- Declarar algunas hipótesis. Por lo general, la hipótesis nula es que la nueva variante "B" no es mejor que la original "A", mientras que la hipótesis alternativa declara lo contrario.
- Determine un tamaño de muestra por adelantado mediante un cálculo de potencia estadística , a menos que esté utilizando enfoques de prueba secuenciales. Utilice una calculadora de tamaño de muestra que tenga en cuenta la potencia estadística, la tasa de conversión actual y el efecto mínimo detectable.
- Ejecute la prueba y espere a que cada variación se exponga al tamaño de muestra predeterminado.
- Calcule la probabilidad de observar un resultado al menos tan extremo como los datos bajo la hipótesis nula (valor p). Rechazar la hipótesis nula e implementar la nueva variante en producción si el valor p < 5 %.
¿Cómo se compara esto con el bayesiano? Vamos a ver…
Pruebas A/B Bayesianas vs Frecuentes
Este es un debate notorio dondequiera que se utilice la inferencia estadística. Y para ser franco, no tiene sentido. Ambos tienen sus méritos y casos en los que son el mejor método para usar.
Al contrario de lo que la mayoría de los promotores en ambos campos le harán pensar, son similares en varios aspectos y ninguno se acerca más a la verdad que el otro, aunque sus enfoques difieren.
Cuando se aplica a las pruebas A/B, por ejemplo, ningún método específico le dará una predicción absoluta y precisa en términos del curso de acción que provocará el crecimiento del negocio. En cambio, las pruebas A/B lo ayudan a eliminar el riesgo de la toma de decisiones.
Independientemente de cómo analice sus datos, utilizando enfoques bayesianos o frecuentistas, puede realizar movimientos con cierto nivel de certeza de que tiene razón.
Y por eso, ambos modelos estadísticos son válidos. Bayesian puede tener una ventaja de velocidad, pero es más exigente computacionalmente que Frequentist.
Mira otras diferencias...
El marco frecuentista
La mayoría de nosotros estamos familiarizados con el enfoque frecuentista de los cursos de introducción a la estadística. Definimos la metodología anterior: desde declarar la hipótesis nula, determinar el tamaño de la muestra, recopilar datos a través de un experimento aleatorio y finalmente observar un resultado estadísticamente significativo.
En el frecuentismo, consideramos que la probabilidad está fundamentalmente relacionada con las frecuencias de los eventos repetidos. Por lo tanto, en un lanzamiento de moneda justo, un Frequentist cree que si adivina con suficiente frecuencia, obtendrá cara el 50% de las veces y lo mismo con cruz.
Mentalidad frecuentista: "Si repito el experimento en las mismas condiciones una y otra vez, ¿cuáles son las posibilidades de que mi método obtenga la respuesta correcta?"
El Marco Bayesiano
Mientras que el enfoque frecuentista trata el parámetro de población para cada variante como una constante (desconocida), el enfoque bayesiano modela cada valor de parámetro como una variable aleatoria con alguna distribución de probabilidad.
Aquí, calcula las distribuciones de probabilidad (y, por lo tanto, los valores esperados) para los parámetros de interés directamente.
Y para modelar la distribución de probabilidad de cada variante, nos basamos en la regla de Bayes para combinar los resultados del experimento con cualquier conocimiento previo que tengamos sobre la métrica de interés. Podemos simplificar los cálculos usando un conjugado previo.
Alex Birkett resumió el algoritmo bayesiano de esta manera:
- Defina la distribución previa que incorpora sus creencias subjetivas sobre un parámetro. El previo puede ser no informativo o informativo.
- Reunir datos.
- Actualice su distribución anterior con los datos utilizando el teorema de Bayes (aunque puede tener métodos bayesianos sin el uso explícito de la regla de Bayes; consulte Bayesiano no paramétrico) para obtener una distribución posterior. La distribución posterior es una distribución de probabilidad que representa sus creencias actualizadas sobre el parámetro después de haber visto los datos.
- Analiza la distribución posterior y resúmela (media, mediana, sd, cuantiles…).
En resumen, el experimentador bayesiano se enfoca en su propia perspectiva y en lo que significa la probabilidad para ellos. Su opinión evoluciona con los datos observados. Los frecuentadores, por otro lado, creen que la respuesta correcta está en alguna parte.

Comprenda que el debate Frequentist vs Bayesian no afecta tanto el análisis posterior a la prueba A / B. Las principales diferencias entre los dos campos están más relacionadas con lo que se puede probar.
Las estadísticas de probabilidad generalmente no se utilizan en gran medida en análisis posteriores. El argumento bayesiano-frecuentista es más aplicable con respecto a la elección de las variables a probar en el paradigma A/B, pero incluso allí, la mayoría de los probadores A/B violan las hipótesis de investigación, la probabilidad y los intervalos de confianza .
Dr. Rob Balon a CXL
Georgi elabora más:
Hay varias calculadoras bayesianas en línea y al menos un importante proveedor de software de pruebas A/B que aplica un motor estadístico bayesiano que utiliza los llamados a priori no informativos (un nombre un poco inapropiado, pero no profundicemos en esto). En la mayoría de los casos, los resultados de estas herramientas coinciden numéricamente con los resultados de una prueba frecuentista sobre los mismos datos. Digamos que la herramienta bayesiana reportará algo como '96% de probabilidad de que B sea mejor que A' mientras que la herramienta frecuentista producirá un valor p de 0.04 que corresponde a un nivel de confianza del 96%.
En una situación como la anterior, que es mucho más común de lo que a algunos les gustaría admitir, ambos métodos conducirán a la misma inferencia y el nivel de incertidumbre será el mismo, incluso si la interpretación es diferente.
¿Qué diría un bayesiano sobre este resultado? ¿Convierte el valor p en una probabilidad posterior adecuada al ver un escenario en el que no hay información previa? ¿O todas estas aplicaciones de las pruebas bayesianas están equivocadas por usar un prior no informativo per se?
Realmente no hay necesidad de elegir un campamento y encontrar un lugar detrás de la cubierta para arrojar piedras al otro campamento. Incluso hay evidencia de que ambos marcos producen los mismos resultados. No importa el camino que elija, el destino probablemente será el mismo. Depende de cómo puedas llegar allí con Frequentist vs Bayesian.
Por ejemplo:
- Hay datos que muestran que las pruebas bayesianas son más rápidas y la opción preferida para experimentos interactivos:
Dado que el paradigma bayesiano permite a los experimentadores cuantificar formalmente las creencias e incorporar conocimientos adicionales, es más rápido que el análisis estadístico tradicional.
En una simulación de prueba Bayesiana A/B, cuando se ajustó el criterio de decisión (es decir, aumentando la tolerancia a los errores), el 75 % de los experimentos concluyeron dentro del 22,7 % de las observaciones requeridas por el enfoque tradicional (a un nivel de significación del 5 %). Y registró solo un 10% de error tipo II. - Bayesian también se considera más indulgente, mientras que Frequentist es reacio al riesgo:
Si bien muchas pruebas de Frequentist usan una significancia estadística del 95%, los bayesianos pueden estar satisfechos con menos que eso. Si una variante tiene un 78 % de posibilidades de vencer al control, dependiendo de la pérdida esperada, podría ser una buena decisión implementar esa variante.
Si se equivoca y la pérdida esperada es inferior al uno por ciento, se trata de un daño bastante insignificante para muchas empresas. Este enfoque rudimentario puede ser más adecuado para la toma de decisiones rápida en escenarios de muy bajo riesgo. - Sin embargo, las simulaciones y los cálculos bayesianos requieren mucho cálculo:
Frequentist, por otro lado, se basa en lápiz y papel. Advertencia: si su herramienta de prueba A/B usa Bayesian y no sabe qué suposiciones se están agregando a sus datos, entonces no puede confiar en la "respuesta" que le da su proveedor. Tómalo con una pizca de sal. Y ejecute su propio análisis.
No todo es sol y arcoíris con Bayesian. Como señala Georgi con esta lista de preguntas:
- "¿Quieres obtener el producto de la probabilidad previa y la función de verosimilitud?"
- "¿Quiere la combinación de probabilidades previas y datos como salida?"
- “¿Quiere que las creencias subjetivas se mezclen con los datos para producir el resultado?” (si se utilizan antecedentes informativos)
- “¿Se sentiría cómodo presentando estadísticas en las que se supone que la información previa es altamente cierta mezclada con los datos reales?”
Todos estos son aspectos de las estadísticas bayesianas, en términos sencillos.
¿Qué le dicen realmente las estadísticas bayesianas en las pruebas A/B?
Diseñó su prueba A/B para brindar información sobre cómo un cambio afecta su métrica de interés, como la tasa de conversión o los ingresos por visitante.
Cuando utiliza una herramienta que funciona con estadísticas bayesianas, es importante comprender lo que significan sus resultados porque "B es el ganador" no significa exactamente lo que la mayoría de la gente piensa que significa.
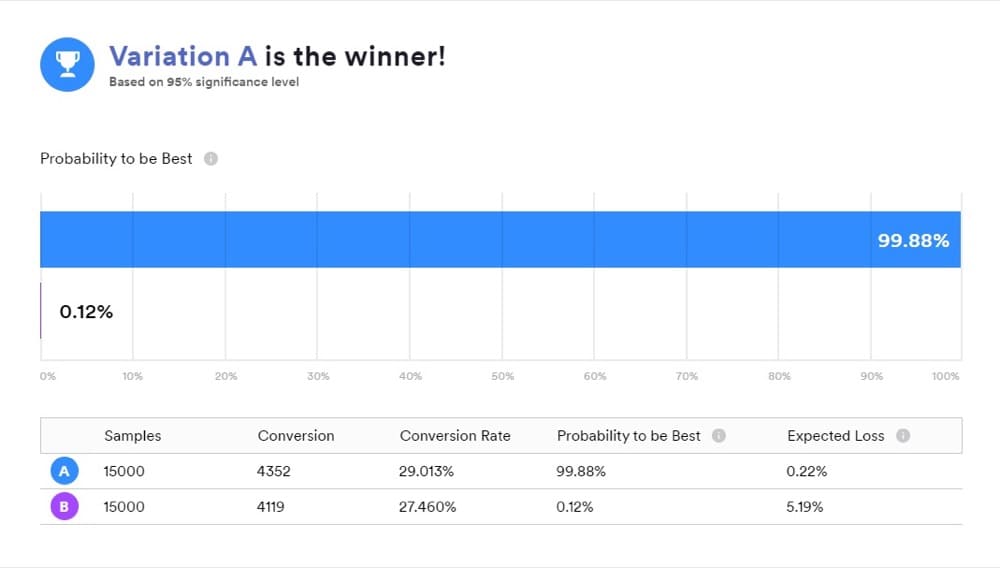
Es una forma conveniente de presentar los resultados, pero eso no es lo que reveló su prueba. En cambio, las respuestas que desea están en comparaciones posteriores de "A" y "B".
Aquí están los 3 métodos de comparación:
Probabilidad de ser el mejor (P2BB)
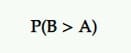
Esta es la probabilidad que declara un ganador en las pruebas Bayesianas A/B.
La variante con probabilidad de ser la mejor es la que tiene mayor probabilidad de seguir superando a la otra.
Esto se calcula a partir de un conjunto de muestras posteriores de la medida de interés del original y del retador.
Entonces, si B tiene la mayor probabilidad de aumentar sus tasas de conversión, por ejemplo, B es declarado ganador.
Aumento esperado
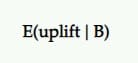
Entonces, si B es el ganador, ¿cuánta mejora deberíamos esperar de él? ¿Continuaría brindando los mismos resultados que vimos en la prueba?
Esa es la perspectiva que el aumento esperado busca proporcionar. El aumento esperado de elegir B sobre A, dado un conjunto de muestras posteriores, se define como el intervalo creíble (o la media) del aumento porcentual.
En las pruebas A/B, generalmente comparamos esto como el retador contra el control. Entonces, si el retador perdió, se representa en valores negativos (como -11,35 %) y valores positivos (como +9,58 %) si ganó.
Pérdida esperada
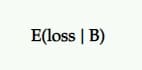
Dado que no hay una probabilidad del 100 % de que B sea mejor que A, existe la posibilidad de registrar una pérdida si elige B sobre A. Esto se representa como pérdida esperada y, al igual que con el aumento esperado, se expresa a partir de la punto de vista del retador contra el control.
Le informa el riesgo de elegir su variante P2BB (es decir, el ganador declarado).
Antes de sumergirnos en los mitos, un enorme agradecimiento a la leyenda de la analítica Georgi Georgiev. Sus análisis en profundidad de la inferencia frecuentista frente a la bayesiana y la probabilidad y estadística bayesianas en las pruebas A/B inspiraron la siguiente sección.
Mitos sobre las estadísticas bayesianas que se deben evitar
Con una rivalidad que es casi tan antigua como innecesaria, el debate bayesiano vs frecuentista ha reunido una gran cantidad de aportes y ha dado lugar a muchos mitos.
El mayor de estos mitos (mito n.º 2) es promovido por los proveedores de herramientas de pruebas A/B para decirle por qué un enfoque es mejor que el otro.
Pero después de leer las secciones anteriores, lo sabes mejor.
Vamos a revelar los agujeros en estos mitos.
Mito n.º 1: los bayesianos afirman sus suposiciones, los frecuentistas no
Esto sugiere que los bayesianos hacen suposiciones en forma de distribuciones previas y están abiertas a evaluación. Pero los Frecuentistas hacen suposiciones que están ocultas en medio de las matemáticas.
Por qué está mal: los bayesianos y los frecuentistas hacen suposiciones subyacentes similares, la única diferencia es que los bayesianos hacen suposiciones adicionales, además de las matemáticas.
Los modelos frecuentistas utilizan suposiciones en las matemáticas, como la forma de la distribución, la homogeneidad o heterogeneidad del efecto entre las observaciones y la independencia de la observación. Y no están ocultos. De hecho, se discuten ampliamente en la comunidad estadística y se establecen para cada prueba estadística frecuentista.
La verdad: los frecuentistas declaran explícitamente sus suposiciones y dan un paso más para probar las suposiciones: pruebas de normalidad, prueba de bondad de ajuste (bajo la cual tenemos la prueba de desajuste de proporción de muestra) y más.
Mito #2. Los métodos bayesianos le brindan las respuestas que realmente desea
El concepto erróneo aquí es que los valores p y los intervalos de confianza no le dicen a los evaluadores lo que quieren saber, mientras que las probabilidades posteriores y los intervalos creíbles sí lo hacen. La gente quiere saber cosas como
- La probabilidad de que B supere a A y
- La probabilidad de que el resultado no sea una coincidencia.
Los valores P y las pruebas de hipótesis (inferencia directa) no proporcionan esa información, pero la inferencia inversa sí.
Por qué está mal: Esta es una cuestión de lingüística. Generalmente, cuando los no estadísticos usan términos como "posibilidad", "azar" y "probabilidad", no los usan teniendo en cuenta su significado técnico. Indague más a fondo y descubrirá que están tan confundidos con la inferencia inversa como con la inferencia directa.
Según Georgi Georgiev, comienzan a surgir preguntas como estas:
- ¿Qué es una probabilidad previa? ¿Qué valor trae?
- "¿Qué es una función de probabilidad?"
- "¿Qué probabilidad 'previa', no tengo datos previos?"
- “¿Cómo defiendo la elección de una probabilidad previa?”
- “¿Hay alguna manera de comunicar exactamente lo que dicen los datos, sin ninguna de estas mezclas?”
La verdad: debería haber una mejor comprensión de lo que los probadores quieren saber, no de su mala interpretación de los términos técnicos. Los valores P, los intervalos de confianza y otros le indican qué tan probados están los resultados con los datos recopilados. Proporcionaron una medida de certeza sin la influencia de supuestos previos subjetivos y no probados.
Mito n.° 3: la inferencia bayesiana lo ayuda a comunicar la incertidumbre mejor que la inferencia frecuentista
Porque los resultados de las pruebas producen ideas más “significativas”.
Por qué está mal: tanto el enfoque frecuentista como el bayesiano tienen herramientas similares para ayudarlo a comunicar certeza y los resultados de su prueba A/B.
| frecuentista | bayesiano | ||||||||||
| ● Estimaciones puntuales | ● Estimaciones puntuales | ||||||||||
| ● valores P | ● Intervalos creíbles | ||||||||||
| ● Intervalos de confianza | ● Factores de Bayes | ||||||||||
| ● Curvas de valor P | ● Distribuciones posteriores (realizar la misma tarea como las curvas Frecuentista) | ||||||||||
| ● Curvas de confianza | |||||||||||
| ● Curvas de gravedad, etc. |
La verdad: Todo depende de cómo los uses. Ambos métodos son igualmente efectivos para comunicar la incertidumbre. Sin embargo, existen diferencias en cómo presentan la medida de incertidumbre.
Mito #4. Los resultados de las pruebas Bayesianas A/B son inmunes a las miradas a escondidas
Algunos estadísticos bayesianos argumentan que puede detener una prueba bayesiana una vez que vea un "ganador claro" y hace poca diferencia en el resultado final.
Probablemente sepa que esto es inaceptable en las pruebas Frequentist, por lo que se cuenta como una desventaja en comparación con Bayesian. ¿Pero es realmente?
Por qué está mal: en un estudio de 1969 en el Journal of the Royal Statistical Society titulado "Pruebas de significación repetidas sobre la acumulación de datos", Armitage et al. mostró cómo la detención opcional basada en resultados aumenta la probabilidad de error.
No puede simplemente detenerse cuando observa un ganador, actualizar su posterior y usarlo como su próximo anterior sin ajustar la forma en que funciona el análisis bayesiano.
La verdad: Peeking afecta la inferencia bayesiana tanto como Frequentist (si quieres hacerlo bien).
Mito #5. Las estadísticas frecuentistas son ineficientes ya que debe esperar un tamaño de muestra fijo
Algunos miembros de la comunidad CRO creen que las pruebas estadísticas frecuentistas deben ejecutarse con un tamaño de muestra fijo y predeterminado, de lo contrario, los resultados no son válidos.
Como resultado, espera más de lo necesario para obtener los resultados que desea.
Por qué está mal: las estadísticas frecuentistas no se han usado de esa manera desde hace unas siete décadas. Con las pruebas secuenciales frecuentistas, no requiere una duración fija predeterminada.
La verdad: las pruebas secuenciales, que son más populares hoy en día, requieren un tamaño de muestra máximo para equilibrar los errores de tipo I y tipo II, pero el tamaño de muestra real utilizado varía de un caso a otro según el resultado observado.
Entonces, ¿debería elegir bayesiano o frecuentista? Hay un Lugar para Ambos.
No hay necesidad de elegir un lado. Ambos métodos tienen su lugar. Por ejemplo, un proyecto a largo plazo que utiliza antecedentes actualizados y necesita resultados rápidos funciona mejor con el enfoque bayesiano.
El método Frequentist, por otro lado, es más adecuado para proyectos que requieren una cantidad significativa de repetibilidad en sus resultados. Por ejemplo, al escribir software que usarán muchas personas con muchos conjuntos de datos.
Como dice Cassie Kozyrkov, Directora de Inteligencia de Decisiones de Google, “La estadística es la ciencia de cambiar de opinión bajo la incertidumbre”.
En su video de resumen Bayesian vs Frequentist Statistics, dijo:
“Puedes tomar ese debate frecuentista y bayesiano y reducirlo todo a lo que estás cambiando de opinión. Los frecuentes cambian de opinión acerca de las acciones, tienen una acción predeterminada preferida, tal vez no tengan ninguna creencia, pero tienen una acción que les gusta bajo la ignorancia y luego preguntan: "¿Mi evidencia [o datos] cambia de opinión sobre esa acción? “¿Me siento ridículo haciéndolo basado en mi evidencia?”
Los bayesianos, por otro lado, cambian de opinión de una manera diferente. Comienzan con una opinión, una opinión personal expresada matemáticamente, llamada anterior, y luego preguntan: "¿Cuál es la opinión sensata que debo tener después de incorporar alguna evidencia?" Y así, los frecuentistas cambian de opinión sobre las acciones, los bayesianos cambian de opinión sobre las creencias.
Y dependiendo de cómo desee enmarcar su toma de decisiones, es posible que prefiera optar por un campo en lugar del otro”.
Al final, todos nos dirigimos hacia conclusiones similares: la diferencia está en cómo se le presentan esas conclusiones.
Si la inferencia frecuentista y bayesiana fueran funciones de programación, y las entradas fueran problemas estadísticos, entonces las dos serían diferentes en lo que devuelven al usuario. La función de inferencia frecuentista devolvería un número, que representa una estimación (normalmente, una estadística de resumen como el promedio de la muestra, etc.), mientras que la función bayesiana devolvería probabilidades.
Extracto del libro “Programación Probabilística y Métodos Bayesianos para Hackers
Lo que no es del todo correcto es la afirmación de que uno da más resultados prácticos que el otro.
Punto clave
Las estadísticas bayesianas en las pruebas A/B consisten en 4 pasos distintos:
- Identifique su distribución anterior
- Elija un modelo estadístico que refleje sus creencias
- Ejecutar el experimento
- Usa los resultados para actualizar tus creencias y calcular una distribución posterior
Sus resultados le indicarán probabilidades perspicaces. Entonces sabrá qué variante tiene la mayor probabilidad de ser la mejor, su pérdida esperada y su mejora esperada.
Estos suelen ser interpretados por la mayoría de las herramientas de prueba A/B que utilizan estadísticas bayesianas. Pero un experimentador minucioso realizará un análisis posterior a la prueba para comprender mejor esos resultados.
Debido a que has llegado hasta aquí, aquí hay un dato divertido para ti: ¿Conoces el retrato de Thomas Bayes con el que todos están familiarizados? Éste:

Nadie está 100% seguro de que sea él.