タイプIおよびタイプIIのエラー：最適化における不可避のエラー

タイプIおよびタイプIIのエラーは、実験で勝者を誤って見つけた場合、または見つけられなかった場合に発生します。 両方のエラーが発生すると、機能しているかどうかに関係なく動作するように見えます。 そして、実際の結果ではありません。

テスト結果を誤って解釈すると、最適化の取り組みが誤って行われるだけでなく、長期的に最適化プログラムが失敗する可能性があります。

これらのエラーをキャッチするのに最適なタイミングは、エラーを作成する前です。 それでは、最適化実験でタイプIおよびタイプIIのエラーが発生しないようにする方法を見てみましょう。

しかしその前に、帰無仮説を見てみましょう…タイプIおよびタイプIIのエラーを引き起こすのは、帰無仮説の誤った棄却または非棄却であるためです。

帰無仮説：H0

実験を仮定するとき、提案された変更が特定のメトリックを移動することを示唆するために直接ジャンプすることはありません。

まず、提案された変更は関連するメトリックにまったく影響を与えない、つまりそれらは無関係であると言うことから始めます。

これは帰無仮説（H0）です。 H0は常に変化がないということです。 これはあなたが信じていることです、デフォルトでは…あなたの実験がそれを反証するまで（そしてもしそうなら）。

そして、対立仮説（HaまたはH1）は、前向きな変化があるというものです。 H0とHaは常に数学的に反対です。 Haは、提案された変更が違いを生むことを期待するものであり、対立仮説です。これは、実験でテストしているものです。

したがって、たとえば、価格設定ページで実験を実行して別の支払い方法を追加する場合は、最初に次のような帰無仮説を立てます。追加の支払い方法は売上に影響を与えません。 対立仮説は次のようになります。追加の支払い方法により、売上が増加します。

実際、実験を実行することは、帰無仮説または現状に挑戦することです。

タイプIおよびタイプIIのエラーは、帰無仮説を誤って棄却または棄却しなかった場合に発生します。

タイプIのエラーを理解する

タイプIの過誤は、誤検知またはアルファエラーとして知られています。

仮説検定のタイプIエラーインスタンスでは、最適化テストまたは実験*は成功したように見えます*。そして、テストしているバリエーションが元のバリエーションとは異なる（良いまたは悪い）ことをしていると（誤って）結論付けます。

タイプIの過誤では、上昇または下降が見られますが、これは一時的なものであり、長期的には維持されない可能性があり、帰無仮説を棄却する（そして対立仮説を受け入れる）ことになります。

帰無仮説を誤って棄却することはさまざまな理由で発生する可能性がありますが、主な理由は、ピークの練習（つまり、中間または実験の実行中に結果を確認すること）です。 そして、設定された停止基準に達するよりも早くテストを呼び出します。

多くのテスト方法では、中間結果を確認すると誤った結論が導き出され、タイプIのエラーが発生する可能性があるため、覗き見の練習は推奨されません。

タイプIエラーを発生させる方法は次のとおりです。

B2B Webサイトのランディングページを最適化しており、バッジや賞を追加すると見込み客の不安が軽減され、フォームの入力率が向上する（結果としてリードが増える）と仮定します。

したがって、この実験の帰無仮説は次のようになります。バッジを追加してもフォームの入力には影響しません。

このような実験の停止基準は、通常、特定の期間および/または設定された統計的有意水準でX変換が発生した後です。 従来、オプティマイザは95％の統計的信頼水準に到達しようとします。これは、ほとんどの最適化実験で十分に低いと見なされるタイプIエラーが発生する可能性が5％になるためです。 一般に、このメトリックが高いほど、タイプIのエラーが発生する可能性は低くなります。

目指す自信のレベルによって、タイプIエラー（α）が発生する確率が決まります。

したがって、95％の信頼水準を目指す場合、αの値は5％になります。 ここで、あなたはあなたの結論が間違っている可能性が5％あることを受け入れます。

対照的に、実験で99％の信頼水準を使用すると、タイプIエラーが発生する確率は1％に低下します。

たとえば、この実験では、焦りすぎて、実験が終了するのを待つのではなく、テストツールのダッシュボード（覗き見！）を1日だけ見てみたとします。 そして、あなたは「見かけの」上昇に気づきます—あなたのフォームの記入率は95％の信頼水準でなんと29.2％上昇しました。

そしてBAM…

…あなたは実験をやめます。

…帰無仮説を棄却します（バッジは売上に影響を与えなかった）。

…対立仮説を受け入れます（バッジが売り上げを押し上げた）。

…そして、アワードバッジ付きのバージョンで実行します。

しかし、その月のリードを測定すると、その数は元のバージョンで報告したものとほぼ同等であることがわかります。 結局、バッジはそれほど重要ではありませんでした。 そして、帰無仮説はおそらく無駄に拒否されました。

ここで起こったことは、実験をすぐに終了し、帰無仮説を棄却し、誤った勝者になってしまい、タイプIのエラーが発生したことです。

実験でのタイプIの過誤の回避

タイプIエラーが発生する可能性を低くする確実な方法の1つは、信頼水準を高くすることです。 5％の統計的有意水準（95％の統計的信頼水準に変換）は許容範囲です。 ここでは、ありそうもない5％の範囲で失敗するため、ほとんどのオプティマイザーが安全に行う賭けです。

高い信頼水準を設定することに加えて、テストを十分に長く実行することが重要です。 テスト期間計算機は、テストを実行する必要がある期間を教えてくれます（特に指定された効果サイズなどを考慮した後）。 実験に意図したコースを実行させると、タイプ1エラーが発生する可能性が大幅に減少します（高い信頼水準を使用している場合）。 統計的に有意な結果に達するまで待つことで、帰無仮説を誤って棄却し、タイプIエラーを犯した可能性が低くなります（通常は5％）。 言い換えると、統計的に有意な結果を得るにはそれが重要であるため、適切なサンプルサイズを使用します。

これで、実験の信頼度（または重要度）に関連するタイプIのエラーについて説明しました。 しかし、テストに忍び寄る可能性のある別のタイプのエラー、タイプIIエラーもあります。

タイプIIエラーを理解する

タイプIIエラーは、フォールスネガティブまたはベータエラーとして知られています。

タイプIのエラーとは対照的に、タイプIIのエラーの場合、実験は*失敗した（または結論が出ない）ように見えます* 。あなたは（誤って）テストしているバリエーションがオリジナル。

タイプIIのエラーでは、実際の上昇または下降を確認できず、帰無仮説を棄却できず、対立仮説を棄却することになります。

タイプIIエラーを発生させる方法は次のとおりです。

上から同じB2BWebサイトに戻る…

したがって、今回は、フォームの上部にGDPRコンプライアンスの免責事項を目立つように追加すると、より多くの見込み客がフォームに記入するように促される（結果としてより多くのリードが得られる）と仮定するとします。

したがって、この実験の帰無仮説は次のようになります。GDPRコンプライアンスの免責事項はフォームの入力に影響を与えません。

また、同じ読み取りの対立仮説： GDPRコンプライアンスの免責事項により、フォームへの入力が増えます。

テストの統計的検出力は、偏差が存在する場合に、元のバージョンとチャレンジャーバージョンのパフォーマンスの違いをどれだけうまく検出できるかを決定します。 従来、オプティマイザは80％の統計的検出力を達成しようとします。これは、このメトリックが高いほど、タイプIIエラーが発生する可能性が低くなるためです。

統計的検出力は0から1の間の値を取り（多くの場合％で表されます）、タイプIIエラーの確率（β）を制御します。 1 –βとして計算されます

テストの統計的検出力が高いほど、タイプIIエラーが発生する可能性は低くなります。

したがって、実験の統計的検出力が10％の場合、タイプIIエラーの影響を非常に受けやすくなります。 一方、実験の統計的検出力が80％の場合、タイプIIエラーが発生する可能性ははるかに低くなります。

繰り返しになりますが、テストを実行しますが、今回はフォームの入力に大きな上昇は見られません。 どちらのバージョンも、ほぼ同様の変換を報告します。 そのため、実験を中止し、GDPRコンプライアンスの免責事項なしで元のバージョンを続行します。

ただし、実験期間のリードデータを深く掘り下げると、両方のバージョン（元のバージョンとチャレンジャー）のリードの数は同じように見えますが、GDPRバージョンでは、数が大幅に増加していることがわかります。ヨーロッパからのリードの。 （もちろん、オーディエンスターゲティングを使用して、ヨーロッパからのリードにのみ実験を表示することもできますが、それは別の話です。）

ここで起こったことは、十分なパワーを達成したかどうかをチェックせずに、テストを早く終了したことでした。タイプIIエラーが発生しました。

実験でのタイプIIエラーの回避

タイプIIエラーを回避するには、高い統計的検出力でテストを実行します。 少なくとも80％の統計的検出力を達成できるように、実験を構成してみてください。 これは、ほとんどの最適化実験で許容できるレベルの統計的検出力です。 これを使用すると、少なくとも80％のケースで、誤った帰無仮説を正しく棄却することができます。

これを行うには、それに追加する要因を調べる必要があります。

これらの最大のものはサンプルサイズです（観察された効果サイズが与えられた場合）。 サンプルサイズは、テストの検出力に直接関係しています。 巨大なサンプルサイズは、高検出力テストを意味します。 特に低MEIの場合、チャレンジャーと元のバージョンの結果の違いを検出する可能性が大幅に低下するため、パワー不足のテストはタイプIIエラーに対して非常に脆弱です（これについては以下で詳しく説明します）。 したがって、タイプIIエラーを回避するには、テストがタイプIIエラーを最小限に抑えるのに十分な電力を蓄積するのを待ちます。 理想的には、ほとんどの場合、少なくとも80％のパワーに到達する必要があります。

もう1つの要因は、実験の対象となる最小関心効果（MEI）です。 MEI（MDEとも呼ばれます）は、問題のKPIで検出する必要のある差異の最小の大きさです。 低いMEIを設定すると（たとえば、1.5％の上昇を狙う）、小さな差異を検出するには（十分な検出力を得るには）かなり大きなサンプルサイズが必要になるため、タイプIIエラーが発生する可能性が高くなります。

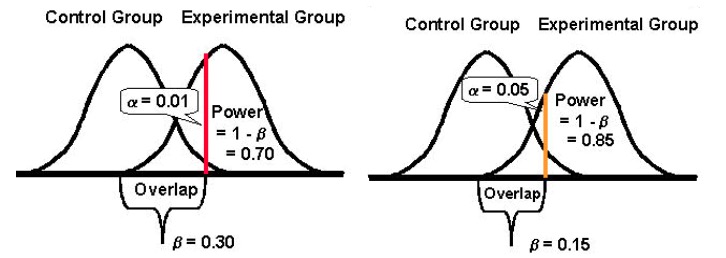
そして最後に、タイプIエラーを発生させる確率（α）とタイプIIエラーを発生させる確率（β）の間には反比例の関係がある傾向があることに注意することが重要です。 たとえば、αの値を減らしてタイプIエラーが発生する確率を下げると（たとえば、αを1％に設定すると、99％の信頼水準を意味します）、実験の統計的検出力（またはその能力β 、存在する場合に差異を検出すること）も減少することになり、それによってタイプIIエラーが発生する可能性が高くなります。

エラーのいずれかをより受け入れやすくする：タイプIおよびII（およびバランスをとる）

あるタイプのエラーの確率を下げると、他のタイプのエラーの確率が高くなります（他のすべてが同じままである場合）。

そのため、どのエラータイプに対してより寛容になる可能性があるかについて電話に出る必要があります。

一方では、タイプIのエラーを作成し、すべてのユーザーに変更を展開すると、コンバージョンと収益にコストがかかる可能性があります。さらに悪いことに、コンバージョンキラーになる可能性もあります。

一方、タイプIIのエラーが発生し、すべてのユーザーに勝利バージョンを展開できなかった場合も、他の方法で獲得できたはずのコンバージョンに費用がかかる可能性があります。

常に、両方のエラーにはコストがかかります。

ただし、実験によっては、一方が他方よりも受け入れられる場合があります。 一般に、テスターは、タイプIのエラーがタイプIIのエラーの約4倍深刻であることに気付きます。

よりバランスの取れたアプローチを取りたい場合は、統計家のJacob Cohenが、「アルファリスクとベータリスクの合理的なバランスを備えた80％の統計的検出力を採用する必要がある」と提案しています。 」（80％の電力は、ほとんどのテストツールの標準でもあります。）

また、統計的有意性に関する限り、基準は95％に設定されています。

基本的に、それは妥協とあなたが許容できるリスクレベルに関するものです。 両方のエラーの可能性を本当に最小限に抑えたい場合は、99％の信頼水準と99％の検出力を使用できます。 しかし、それはあなたが永遠に長いように見える期間の間、信じられないほど巨大なサンプルサイズで作業していることを意味します。 その上、それでも、エラーの余地を残すことになります。

たまに、あなたは実験を間違って結論付けるでしょう。 ただし、これはテストプロセスの一部です。A/Bテストの統計をマスターするには時間がかかります。 成功または失敗した実験を調査して再テストまたはフォローアップすることは、結果を再確認したり、間違いを発見したりする1つの方法です。