Python上の単一ニューロンニューラルネットワーク–数学的直感

非常に単純ですが、完全なネットワークである単純なネットワークを単一のレイヤーで構築しましょう。 1つの入力と1つのニューロン（これも出力です）、1つの重み、1つのバイアスのみ。

最初にコードを実行してから、部分的に分析してみましょう

Githubプロジェクトのクローンを作成するか、お気に入りのIDEで次のコードを実行します。

IDEの設定についてサポートが必要な場合は、ここでプロセスについて説明しました。

すべてがうまくいけば、次の出力が得られます。

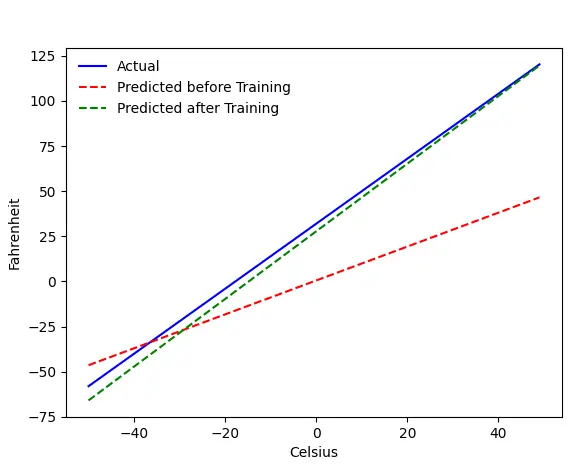
問題—摂氏からの華氏

摂氏から華氏を予測するようにマシンをトレーニングします。 コード（またはグラフ）から理解できるように、青い線は実際の摂氏と華氏の関係です。 赤い線は、トレーニングなしでベビーマシンによって予測された関係です。 最後に、マシンをトレーニングします。緑色の線は、トレーニング後の予測です。

Line＃65–67を見てください—トレーニングの前後で、同じ関数（ get_predicted_fahrenheit_values（） ）を使用して予測しています。 では、魔法のtrain（）は何をしているのでしょうか？ 確認してみましょう。

ネットワーク構造

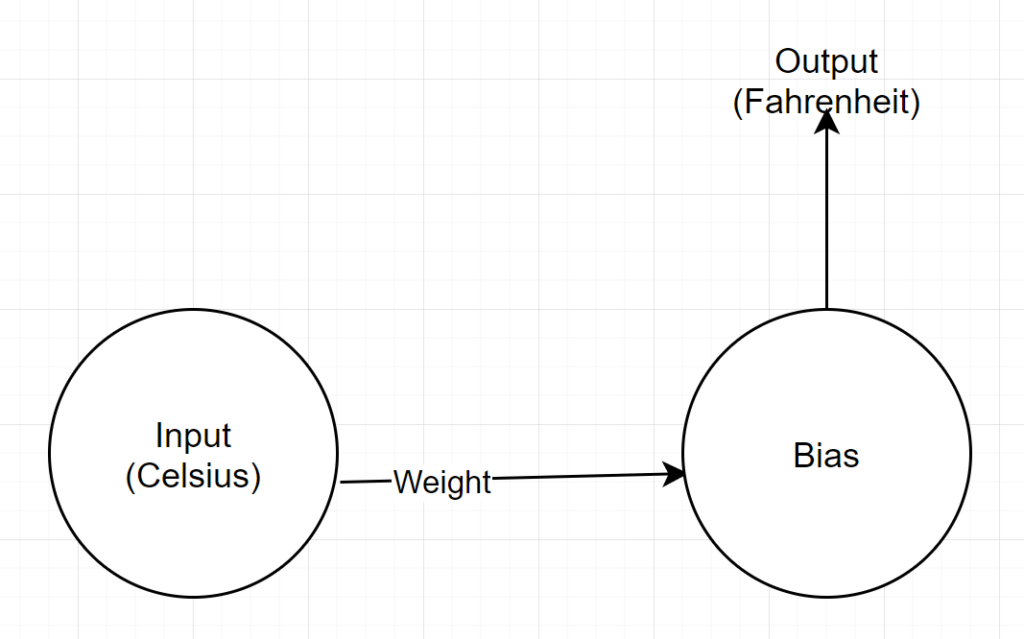
入力：摂氏を表す数値

重量：重量を表すフロート

バイアス：バイアスを表すフロート

出力：予測される華氏を表すフロート

したがって、合計2つのパラメーターがあります—1つの重みと1つのバイアス

コード分​​析

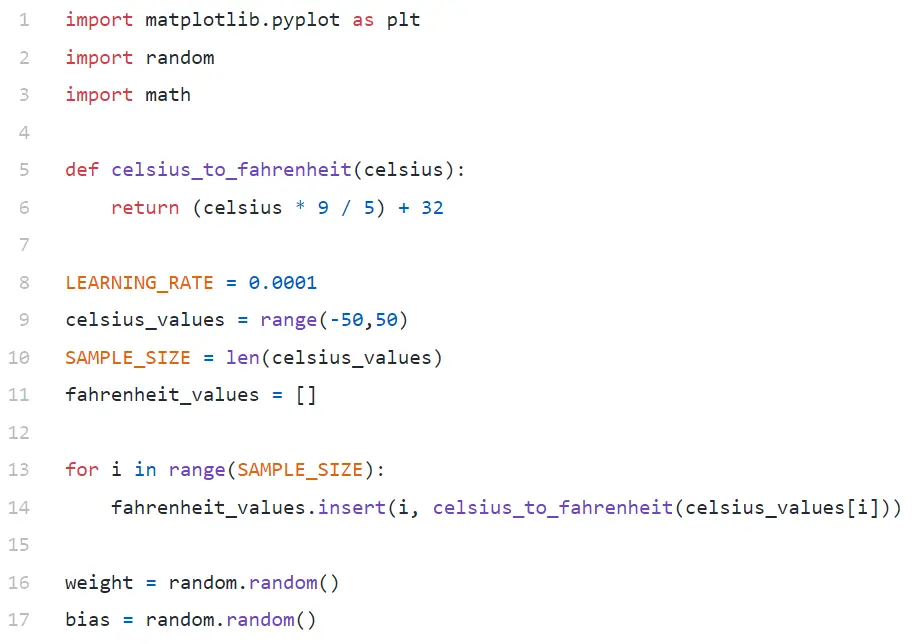
Line＃9では、-50から+50までの100個の数値の配列を生成しています（50を除く—範囲関数は上限値を除外します）。

Line＃11–14では、摂氏値ごとに華氏を生成しています。

行＃16と＃17では、重みとバイアスを初期化しています。

訓練（）

ここでは、10000回のトレーニングを実行しています。 各反復は次のもので構成されます。

1. フォワード（Line＃57）パス
2. 後方（Line＃58）パス
3. update_parameters（Line＃59）

Pythonを初めて使用する場合は、少し奇妙に見えるかもしれません—Python関数は複数の値をタプルとして返すことがあります。

関心があるのはupdate_parametersだけであることに注意してください。ここで行う他のすべては、この関数のパラメーターを評価することです。これは、重みとバイアスの勾配（勾配とは何かを以下で説明します）です。

1. grad_weight：重みの勾配を表すフロート
2. grad_bias：バイアスの勾配を表すフロート

これらの値は逆方向に呼び出すことで取得しますが、出力が必要です。出力は、行＃57で順方向に呼び出すことで取得します。

前方（）

ここで、 celsius_valuesとfahrenheit_valuesは100行の配列であることに注意してください。

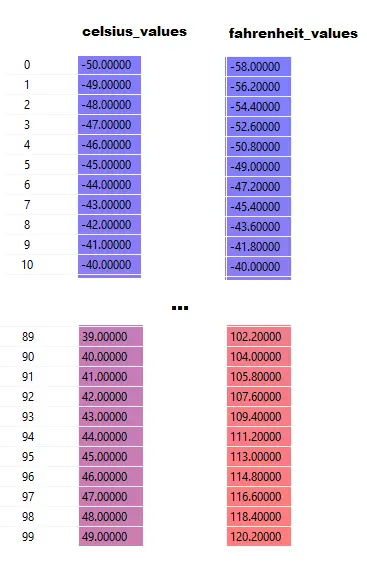
Line＃20–23を実行した後、摂氏値の場合、たとえば42

出力= 42 *重量+バイアス

したがって、 celsius_valuesの100要素の場合、出力は、対応する摂氏値ごとに100要素の配列になります。

Line＃25–30は、平均二乗誤差（MSE）損失関数を使用して損失を計算しています。これは、すべての差の2乗をサンプル数（この場合は100）で割ったものです。

損失が小さいということは、より良い予測を意味します。 すべての反復で印刷損失を維持すると、トレーニングが進むにつれて損失が減少していることがわかります。

最後に、Line＃31では、予測された出力と損失を返します。

後方

ウェイトとバイアスを更新することだけに関心があります。 これらの値を更新するには、それらの勾配を知る必要があり、それがここで計算しているものです。

勾配が逆の順序で計算されていることに注意してください。 出力の勾配が最初に計算され、次に重みとバイアスが計算されるため、「バックプロパゲーション」という名前が付けられています。 その理由は、重みとバイアスの勾配を計算するには、出力の勾配を知る必要があるためです。これにより、連鎖律の式で使用できるようになります。

それでは、グラデーションと連鎖律とは何かを見てみましょう。

勾配

簡単にするために、 celsius_valuesとfahrenheit_valuesの値がそれぞれ42と107.6の1つだけであると考えてください。

ここで、Line＃30の計算の内訳は次のようになります。

損失=（107.6 —（42 *重量+バイアス））²/ 1

ご覧のとおり、損失は2つのパラメーター（重みとバイアス）に依存します。 重量を考慮してください。 想像してみてください。ランダムな値、たとえば0.8で初期化し、上記の式を評価した後、損失の値として123.45を取得します。 この損失値に基づいて、ウェイトを更新する方法を決定する必要があります。 0.9にするべきですか、それとも0.7にするべきですか？

次の反復で損失の値が低くなるように重みを更新する必要があります（損失を最小限に抑えることが最終的な目標であることを忘れないでください）。 したがって、体重を増やすと損失が増える場合は、体重を減らします。 そして、体重を増やすことで損失が減るなら、私たちはそれを増やします。

さて、問題は、重みを増やすと損失が増えるか減るかをどうやって知るかということです。 これがグラデーションの出番です。 大まかに言えば、勾配は導関数によって定義されます。 高校の微積分から、∂y/∂x（xに関するyの偏導関数/勾配）は、xの小さな変化でyがどのように変化するかを示していることを思い出してください。

∂y/∂xが正の場合、xを少し増やすとyが増えることを意味します。

∂y/∂xが負の場合、xを少し増やすとyが減少することを意味します。

∂y/∂xが大きい場合、xの小さな変化はyの大きな変化を引き起こします。

∂y/∂xが小さい場合、xの小さな変化はyの小さな変化を引き起こします。

したがって、グラデーションから2つの情報を取得します。 パラメータを更新する必要がある方向（増加または減少）とその量（大きいまたは小さい）。

連鎖法則

非公式に言えば、連鎖律は次のように述べています。

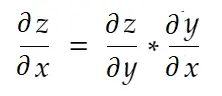
上記の重量の例を考えてみましょう。 この重みを更新するには、 grad_weightを計算する必要があります。これは次のように計算されます。

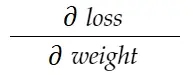
連鎖律の公式で、私たちはそれを導き出すことができます：

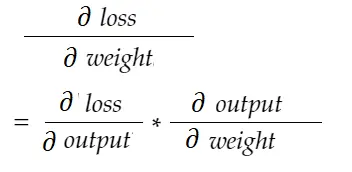
同様に、バイアスの勾配：

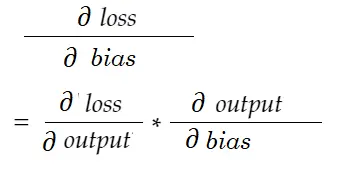
依存関係図を描きましょう。

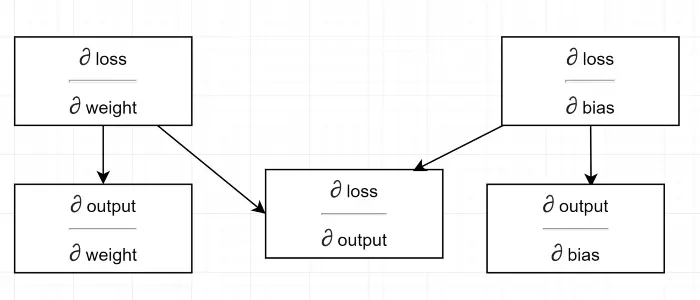
すべての計算は出力の勾配（∂損失/∂出力）に依存することを確認してください。 そのため、最初にバックパスで計算しています（行＃34–36）。

実際、PyTorchなどの高レベルのMLフレームワークでは、バックパスのコードを記述する必要はありません。 フォワードパスでは計算グラフを作成し、バックパスではグラフの反対方向を通過し、連鎖律を使用して勾配を計算します。

∂損失/∂出力

この変数は、行＃34–36で計算したコードのgrad_outputによって定義します。 コードで使用した式の背後にある理由を調べてみましょう。

マシン内の100個のcelsius_valuesすべてを一緒にフィードしていることを忘れないでください。 したがって、grad_outputは100個の要素の配列になり、各要素にはcelsius_valuesの対応する要素の出力の勾配が含まれます。 簡単にするために、 celsius_valuesには2つの項目しかないことを考えてみましょう。

だから、ライン＃30を分解すると、

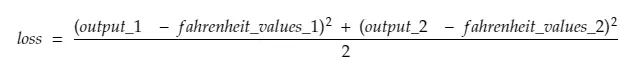
どこ、

output_1=1番目の摂氏値の出力値

output_2=2番目の摂氏値の出力値

fahreinheit_values_1=1番目の摂氏値の実際のfahreinheit値

fahreinheit_values_1=2番目の摂氏値の実際のfahreinheit値

これで、結果の変数grad_outputには、output_1とoutput_2の勾配という2つの値が含まれます。これは、次のことを意味します。

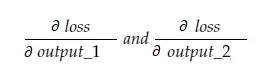
output_1の勾配のみを計算して、他のルールにも同じルールを適用できます。

微積分時間！

これはline＃34–36と同じです。

重量勾配

想像してみてください。celsius_valuesには要素が1つだけあります。 今：

これはLine＃38–40と同じです。 100 celsius_valuesの場合、各値のグラデーション値が合計されます。 明らかな質問は、なぜ結果を縮小しないのか（つまり、SAMPLE_SIZEで除算しないのか）です。 パラメーターを更新する前にすべての勾配に小さな係数を掛けているので、それは必要ありません（最後のセクション「パラメーターの更新」を参照）。

バイアス勾配

これはLine＃42と同じです。 重み勾配と同様に、100個の入力のそれぞれのこれらの値が合計されています。 繰り返しになりますが、パラメータを更新する前に勾配が小さな係数で乗算されるため、問題ありません。

パラメータの更新

最後に、パラメータを更新しています。 トレーニングを安定させるために、減算される前に勾配に小さな係数（LEARNING_RATE）が掛けられていることに注意してください。 LEARNING_RATEの値が大きいとオーバーシュートの問題が発生し、値が極端に小さいとトレーニングが遅くなり、より多くの反復が必要になる場合があります。 試行錯誤しながら、最適な値を見つける必要があります。 レートの学習について詳しく知るために、これを含む多くのオンラインリソースがあります。

調整する正確な量はそれほど重要ではないことに注意してください。 たとえば、LEARNING_RATEを少し調整すると、 descent_grad_weight変数とdescent_grad_bias変数（Line＃49–50）は変更されますが、マシンは引き続き機能する可能性があります。 重要なことは、これらの量が同じ係数（この場合はLEARNING_RATE）でグラデーションを縮小することによって得られることを確認することです。 言い換えれば、「勾配の降下を比例的に保つ」ことは、「勾配の降下量」よりも重要です。

また、これらの勾配値は、実際には100個の入力のそれぞれについて評価された勾配の合計であることに注意してください。 ただし、これらは同じ値でスケーリングされるため、上記のように問題ありません。

パラメータを更新するには、globalキーワード（Line＃47）でパラメータを宣言する必要があります。

ここからどこへ行くか

forループをPythonの方法でリスト内包表記に置き換えることで、コードははるかに小さくなります。 今それを見てください—理解するのに数分以上かかることはありません。

これまでのすべてを理解している場合は、おそらく、複数のニューロン/レイヤーを備えた単純なネットワークの内部を確認する良い機会です。ここに記事があります。