正規分布–数学を使わない直感的な紹介

公開: 2021-06-28

私は、この記事を方程式や一口の専門用語からできるだけ解放するように努めます。ただし、少なくとも次の機能が必要です。

簡単なグラフを解釈することができます。
確率の初級レベルの知識。少なくとも、私がコインを投げた場合、頭には50％の確率があることを理解しています。
積分微積分と量子物理学（冗談です！）

なぜ正規分布なのか

何かを理解する直感的な方法は、それが必要な理由を調査することです。正規分布（ガウス分布とも呼ばれます）でそれを実行しましょう。

あなたが面白い習慣を持っているとしましょう。毎日100回コインを投げます。頭が50回、または1日のほとんどの場合50回近くになると予想するのは「正常」です。まれに、頭に良い日があります— 55回程度になることもありますが、65回を超えることはめったにありません。

ここで、この「希少性」を定量化する必要があります。だから、あなたはあなたが毎日何回頭を手に入れたのかを追跡し始めます。

年間の毎日の頭の数

以下は1年後（365日）のデータです。最初のデータは初日に獲得した頭の数であり、最後のデータは最終日に獲得した頭の数です。以下のすべての数値を確認する必要はありませんが、それらのほとんどが約50であることが簡単にわかります。

56、47、54、50、57、51、57、48、54、62、42、51、37、42、50、37、59、48、46、51、61、47、46、48、63、 55、50、50、43、46、56、49、50、54、52、47、51、59、61、53、44、53、59、58、54、54、50、49、51、46、 43、51、49、54、46、44、41、51、51、49、64、46、46、46、52、48、57、49、42、46、55、50、52、51、47、 53、50、48、58、43、60、49、46、42、53、45、57、48、52、47、47、47、42、57、60、49、48、50、51、47、 48、52、47、45、51、55、51、45、46、46、40、52、57、48、51、48、44、46、41、59、60、46、44、36、48、 52、49、49、49、51、41、49、51、51、42、51、45、54、50、48、49、43、52、53、52、53、48、37、53、54、 41、48、52、46、47、57、50、49、46、57、67、50、54、48、50、60、43、49、57、57、45、55、57、52、46、 48、49、51、45、48、44、48、55、51、59、52、50、55、51、46、48、51、46、50、49、50、47、51、43、46、 48、56、47、57、44、54、52、55、46、49、53、40、54、54、49、50、53、41、55、50、42、58、47、53、55、 45、52、61、50、49、48、51、50、56、44、47、45、48、63、43、52、55、46、48、52、49、56、62、57、54、 47、51、52、43、45、57、51、46、42、52、57、54、48、54、51、49、51、42、52、50、52、61、61、44、45、 48、49、48、46、47、57、44、44、47、52、47、42、48、51、58、36、57、53、49、52、50、52、56、44、56、 46、42、46、43、56、49、44、38、46、52、49、58、51、49、48、52、57、43、48、40、52、54、40、54、45、 49、41、57、50、52、43、54、49、45、44、53、49、43、51、50、56、45、46、47、41、52、59、52、50、48、 58、52、51、55、49、41、38、57、56、41、54、44、47、60、44

ヒストグラムでよりよく視覚化する

上記のデータからヒストグラムをプロットしてみましょう。

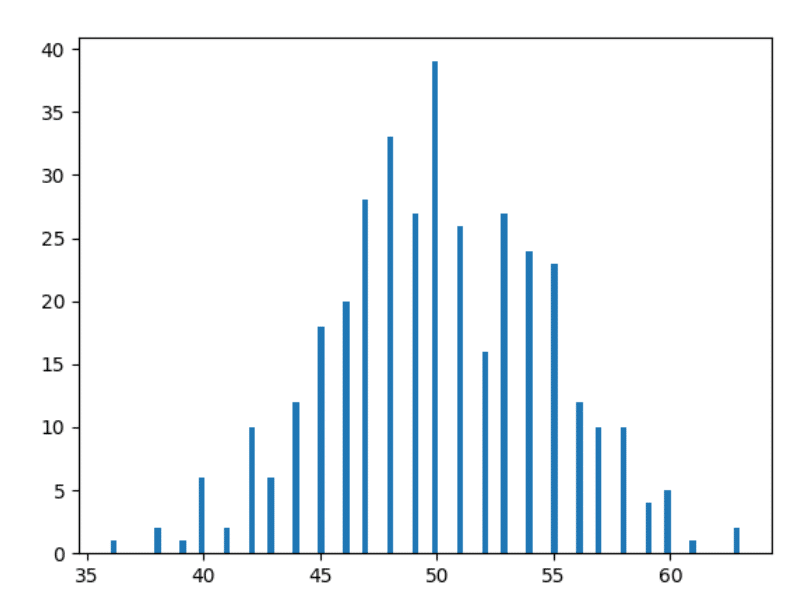
あはは！「正規分布」をググってみたときにインターネットで見た画像のように見えませんか？私たちは、ほぼ、そこにいる！

したがって、ヒストグラムを理解していない場合は、ここで、特定の頭数を取得した日数をプロットしました。たとえば、1年の特定の2日間に36回頭を取得しました（信じられない場合は上のデータを確認してください）。そのため、36の水平点（赤）に高さ2単位のバーがあります。下の画像の左側にある長方形）。

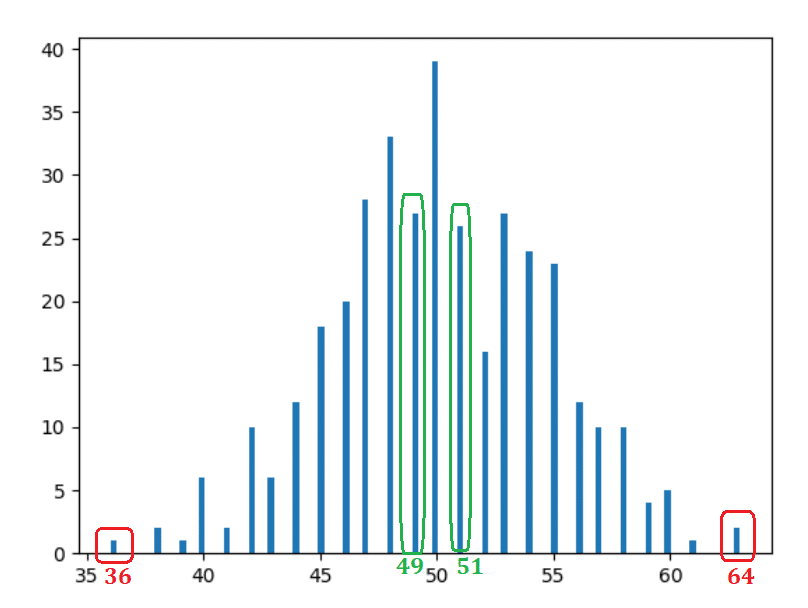
観察

かなり明白で予想されます—ほとんどの場合50頭が発生しました。
中心（50）から離れるほど、発生はほとんど減少しています。
同じ距離にあるバーは同じような形をしています。たとえば、1つのユニットを左（49）または右（51）に移動すると、発生は同様になります—それぞれ30と31（緑色の長方形）。 14ユニットを左（36）または右（64）に移動すると、発生は再び同様になります—それぞれ2と1（赤い長方形）。

10年のデータ

それでは、少し早送りして、10年分のデータをプロットしましょう。

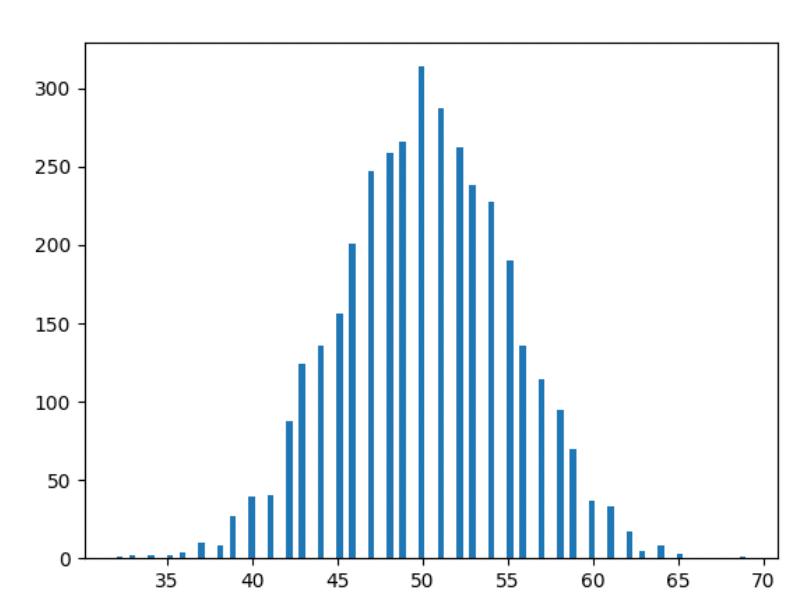
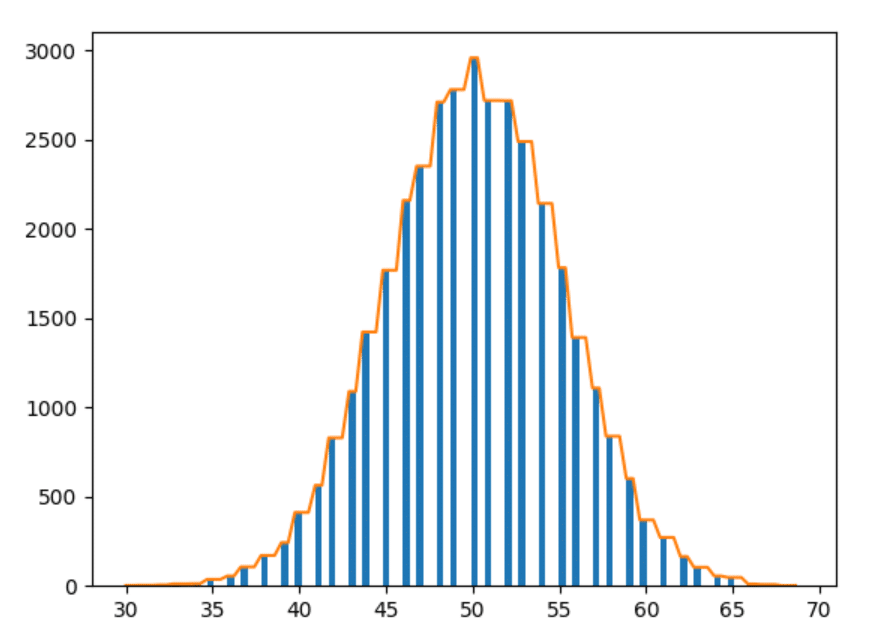
1000年のデータ

わかりました—最後の1つです。 1000年のデータをプロットしてみましょう。

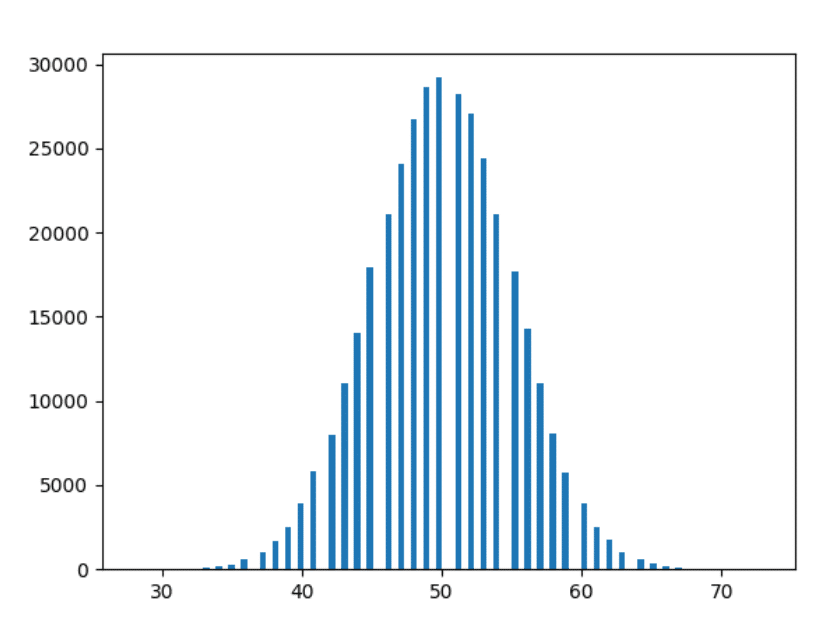
観察

実験すればするほど、形は滑らかになります。
実験を重ねるほど、上記の観察結果に沿ったバーが増えます（つまり、同じ距離にあるバーはより近い形状になります）。

ひどい正規分布はどこにありますか

さて、背景が多すぎます。それでは、要点を説明しましょう。

Googleが提案した答えを見てみましょう：

この定義のいくつかのこと：

確率変数：簡単に言えば、確率変数は、コイントスのようなランダムな実験の可能な値のセットです。この例では、実験の可能な値はHeadまたはTailです。

ベル型：ヒストグラムがベル型になっていることに気づきましたか？

対称：同じ距離にあるバーは似たような形をしています—対称ではありませんか？

したがって、正規分布は、コイントスなどのイベントの結果の分布を表します。この分布では、対称性やベルの形状など、いくつかのプロパティが維持される傾向があります。

コイントス以外のどのような現象が正規分布に従いますか？

ここにいくつかのクールな例があります。

人口の身長—より多くの人々が平均身長グループに分類されます。非常に背の高い人や非常に背の低い人を見つけることはめったにありません。そして、非常に高いものと非常に短いものを見つける可能性はほぼ同じです。
サイコロを振る
靴のサイズ
IQ
そして他にもたくさん…

これらの現象は厳密に正規分布に従いますか？

簡単な答えはノーです。ただし、上記で見たように、実験を重ねるほど、データは正規分布のプロパティに従います。しかし、ありそうもないイベントがとにかく発生しないという保証はありません。

宇宙のすべての確率分布は正規分布ですか？

いいえ。他の種類の分布によって決定される多くの現象があります。

特定の数の顧客が到着する確率、電話、事故、スポーツイベント、および洪水は、ポアソン分布に従います。
事業売上高については、企業の顧客の20％が売上高の80％を占めています。（パレート分布）
都市の交通パターン—指数分布
女の子と男の子の母集団からのチームのメンバーのランダムな選択—超幾何分布

などなど …

上記のリストは、ここにリストされているいくつかのディストリビューションを使用して「実際の例」をグーグルで検索するだけで作成しました。すべてを理解しているわけではありません。 😉

一部の自然現象が正規分布に従う傾向がある理由はありますか

はい—私のお気に入りの説明を引用します：

通常の説明は、「エラー分布」である正規分布の別名で与えられます。エラーは一般にランダムであるため、他の方向と同じように一方向に進む可能性が高いという考え方です。たとえば、射手は少し左に、少し右に、または少し高く、少し低く撃つ可能性があります。したがって、ショットがブルズアイからどれだけ離れているかのグラフは、このランダムな傾向を反映し、平均を中心に対称になります。同様に、身長と知性により、栄養、病気、低所得などの多くの環境要因と同様に、多くの遺伝子（おそらく数千）がこれらの結果に寄与します。

正規分布のパラメーター

これまでの議論の直感を理解した場合—あなたはすでに勝者です。任務完了。記事の残りの部分はボーナスです。

表示されるすべての正規分布グラフは、形状が異なります。それらのいくつかは他のものより平らです。それらのいくつかは良い高さを持っています。これらの形状はすべて、次の2つのパラメータによってのみ制御されます。

平均

平均は平均によって定義されます。ベルの高さを定義します。コイントスの例では、平均は50に近く、これはグラフの一番上の位置です。

標準偏差

この記事には方程式がないことを約束しているので、ここではその数学的表現を示していません。しかし、とにかくそれはそれほど難しいことではありません。標準偏差は、データの多様性を表す指標です。

たとえば、サッカーファンクラブでは最年少グループと最年長グループの年齢差がはるかに大きいため、育児の年齢の標準偏差はサッカーファンクラブの年齢の標準偏差よりも低くなります。

標準偏差は曲線の幅を決定します。標準偏差が小さいと曲線が急になり、標準偏差が大きいと曲線が平坦になります。