Fehler 1. und 2. Art: Die unvermeidlichen Fehler bei der Optimierung

Fehler vom Typ I und Typ II treten auf, wenn Sie in Ihren Experimenten fälschlicherweise Gewinner erkennen oder sie nicht erkennen. Bei beiden Fehlern entscheiden Sie sich für das, was zu funktionieren scheint oder nicht. Und nicht mit den realen Ergebnissen.

Die Fehlinterpretation von Testergebnissen führt nicht nur zu fehlgeleiteten Optimierungsbemühungen, sondern kann Ihr Optimierungsprogramm langfristig zum Scheitern bringen.

Die beste Zeit, um diese Fehler zu erkennen, ist, bevor Sie sie überhaupt machen! Sehen wir uns also an, wie Sie vermeiden können, bei Ihren Optimierungsexperimenten auf Fehler vom Typ I und Typ II zu stoßen.

Aber schauen wir uns vorher die Nullhypothese an … denn es ist die irrtümliche Zurückweisung oder Nicht-Zurückweisung der Nullhypothese, die Fehler vom Typ I und Typ II verursacht .

Die Nullhypothese: ​H0

Wenn Sie für ein Experiment eine Hypothese aufstellen, schlagen Sie nicht direkt vor, dass die vorgeschlagene Änderung eine bestimmte Metrik verschieben wird.

Sie beginnen damit, dass Sie sagen, dass die vorgeschlagene Änderung überhaupt keine Auswirkungen auf die betreffende Metrik hat – dass sie nichts miteinander zu tun haben.

Dies ist Ihre Nullhypothese (H0). H0 ist immer, dass es keine Veränderung gibt. Dies ist, was Sie standardmäßig glauben … bis (und falls) Ihr Experiment es widerlegt.

Und Ihre alternative Hypothese (Ha oder H1) ist, dass es eine positive Veränderung gibt. H0 und Ha sind immer mathematische Gegensätze. Ha ist diejenige, bei der Sie erwarten, dass die vorgeschlagene Änderung einen Unterschied macht, es ist Ihre Alternativhypothese – und die testen Sie mit Ihrem Experiment.

Wenn Sie beispielsweise auf Ihrer Preisseite ein Experiment durchführen und eine weitere Zahlungsmethode hinzufügen möchten, würden Sie zunächst eine Nullhypothese bilden, die besagt: Die zusätzliche Zahlungsmethode hat keine Auswirkungen auf den Umsatz. Ihre alternative Hypothese würde lauten: Die zusätzliche Zahlungsmethode WIRD den Umsatz steigern.

Ein Experiment durchzuführen bedeutet in der Tat, die Nullhypothese oder den Status quo in Frage zu stellen.

Fehler vom Typ I und Typ II treten auf, wenn Sie die Nullhypothese fälschlicherweise ablehnen oder nicht ablehnen.

Fehler 1. Art verstehen

Fehler vom Typ I sind als Fehlalarme oder Alpha-Fehler bekannt.

Bei einem Hypothesentest mit Fehler 1. Art scheint Ihr Optimierungstest oder -experiment * ERFOLGREICH ZU SEIN* und Sie kommen (fälschlicherweise) zu dem Schluss, dass die von Ihnen getestete Variante anders (besser oder schlechter) abschneidet als das Original.

Bei Fehlern erster Art sehen Sie Anstiege oder Einbrüche – die nur vorübergehend sind und auf lange Sicht wahrscheinlich nicht bestehen bleiben – und enden damit, Ihre Nullhypothese abzulehnen (und Ihre Alternativhypothese zu akzeptieren).

Das irrtümliche Zurückweisen der Nullhypothese kann aus verschiedenen Gründen geschehen, aber der Hauptgrund ist die Praxis des Peeking (dh das Betrachten Ihrer Ergebnisse in der Zwischenzeit oder während das Experiment noch läuft). Und das Aufrufen der Tests früher als das festgelegte Abbruchkriterium erreicht ist.

Viele Testmethoden raten von der Praxis des Peeking ab, da das Betrachten von Zwischenergebnissen zu falschen Schlussfolgerungen führen könnte, die zu Fehlern erster Art führen könnten.

So könnten Sie einen Typ-I-Fehler machen:

Angenommen, Sie optimieren die Zielseite Ihrer B2B-Website und stellen die Hypothese auf, dass das Hinzufügen von Abzeichen oder Auszeichnungen die Angst Ihrer potenziellen Kunden verringert und dadurch Ihre Formularausfüllrate erhöht (was zu mehr Leads führt).

Ihre Nullhypothese für dieses Experiment lautet also: Das Hinzufügen von Badges hat keinen Einfluss auf das Ausfüllen von Formularen.

Das Stoppkriterium für ein solches Experiment ist normalerweise ein bestimmter Zeitraum und/oder nachdem X Conversions auf dem festgelegten statistischen Signifikanzniveau stattfinden. Herkömmlicherweise versuchen Optimierer, die statistische Konfidenzmarke von 95 % zu erreichen, da Sie damit eine Wahrscheinlichkeit von 5 % haben, den Typ-I-Fehler zu machen, der für die meisten Optimierungsexperimente als niedrig genug angesehen wird. Im Allgemeinen gilt: Je höher diese Metrik ist, desto geringer ist die Wahrscheinlichkeit, Fehler erster Art zu machen.

Das Vertrauensniveau, das Sie anstreben, bestimmt, wie hoch Ihre Wahrscheinlichkeit ist, einen Fehler 1. Art (α) zu bekommen.

Wenn Sie also ein Konfidenzniveau von 95 % anstreben, beträgt Ihr Wert für α 5 %. Hier akzeptieren Sie, dass Ihre Schlussfolgerung mit einer Wahrscheinlichkeit von 5 % falsch sein könnte.

Wenn Sie dagegen bei Ihrem Experiment mit einem Konfidenzniveau von 99 % vorgehen, sinkt Ihre Wahrscheinlichkeit, einen Fehler 1. Art zu erhalten, auf 1 %.

Angenommen, Sie werden für dieses Experiment zu ungeduldig und anstatt auf das Ende Ihres Experiments zu warten, schauen Sie sich das Dashboard Ihres Testtools an (einen Blick darauf werfen!), nur einen Tag später. Und Sie bemerken einen „offensichtlichen“ Anstieg – dass Ihre Formularausfüllrate um satte 29,2 % mit einem Vertrauensgrad von 95 % gestiegen ist.

Und BAMM…

… du beendest dein Experiment.

… verwerfen die Nullhypothese (dass Badges keinen Einfluss auf den Umsatz hatten).

… die Alternativhypothese akzeptieren (dass Badges den Umsatz ankurbeln).

… und laufen mit der Version mit den Auszeichnungsabzeichen.

Aber wenn Sie Ihre Leads im Laufe des Monats messen, stellen Sie fest, dass die Zahl fast vergleichbar mit dem ist, was Sie mit der Originalversion gemeldet haben. Die Abzeichen waren schließlich nicht so wichtig. Und dass die Nullhypothese wohl vergebens verworfen wurde.

Was hier passiert ist, ist, dass Sie Ihr Experiment zu früh beendet und die Nullhypothese verworfen haben und mit einem falschen Gewinner gelandet sind – einen Typ-I-Fehler gemacht haben.

Vermeidung von Fehlern 1. Art in Ihren Experimenten

Eine sichere Möglichkeit, Ihre Chancen auf einen Fehler erster Art zu verringern, besteht darin, mit einem höheren Konfidenzniveau zu gehen. Ein statistisches Signifikanzniveau von 5 % (was einem statistischen Konfidenzniveau von 95 % entspricht) ist akzeptabel. Es ist eine Wette, die die meisten Optimierer sicher eingehen würden, denn hier werden Sie im unwahrscheinlichen 5%-Bereich scheitern.

Neben der Festlegung eines hohen Konfidenzniveaus ist es wichtig, Ihre Tests lange genug laufen zu lassen. Testdauerrechner können Ihnen sagen, wie lange Sie Ihren Test durchführen müssen (unter anderem nach Berücksichtigung von Dingen wie einer bestimmten Effektgröße). Wenn Sie ein Experiment seinen beabsichtigten Verlauf laufen lassen, verringern Sie die Wahrscheinlichkeit, dass ein Fehler vom Typ 1 auftritt, erheblich (vorausgesetzt, Sie verwenden ein hohes Konfidenzniveau). Wenn Sie warten, bis Sie statistisch signifikante Ergebnisse erzielen, stellen Sie sicher, dass nur eine geringe Wahrscheinlichkeit (normalerweise 5 %) besteht, dass Sie die Nullhypothese fälschlicherweise zurückgewiesen und einen Fehler erster Art begangen haben. Mit anderen Worten, verwenden Sie eine gute Stichprobengröße, da dies entscheidend ist, um statistisch signifikante Ergebnisse zu erhalten.

Nun, das war alles über Typ-I-Fehler, die sich auf das Vertrauensniveau (oder die Signifikanz) Ihrer Experimente beziehen. Aber es gibt noch eine andere Art von Fehlern, die sich in Ihre Tests einschleichen können – die Typ-II-Fehler.

Fehler vom Typ II verstehen

Fehler vom Typ II sind als falsch negative oder Beta-Fehler bekannt.

Im Gegensatz zum Fehler 1. Art scheint das Experiment im Fall eines Fehlers 2. Art * NICHT ERFOLGREICH (ODER NICHT ERFOLGREICH) ZU SEIN* und Sie kommen (fälschlicherweise) zu dem Schluss, dass sich die von Ihnen getestete Variante nicht von der unterscheidet Original.

Bei Fehlern vom Typ II sehen Sie die wirklichen Anstiege oder Einbrüche nicht und lehnen am Ende die Nullhypothese nicht und die Alternativhypothese ab.

So könnten Sie den Typ-II-Fehler machen:

Zurück zur gleichen B2B-Website von oben…

Nehmen wir dieses Mal an, dass Sie die Hypothese aufstellen, dass das Hinzufügen eines Haftungsausschlusses zur DSGVO-Konformität oben auf Ihrem Formular mehr potenzielle Kunden dazu anregen wird, es auszufüllen (was zu mehr Leads führt).

Daher lautet Ihre Nullhypothese für dieses Experiment: Der Haftungsausschluss zur Einhaltung der DSGVO wirkt sich nicht auf das Ausfüllen von Formularen aus.

Und die alternative Hypothese für dasselbe lautet: Der Haftungsausschluss zur Einhaltung der DSGVO führt zu mehr Formularausfüllungen.

Die statistische Aussagekraft eines Tests bestimmt, wie gut er Unterschiede in der Leistung Ihrer Original- und Challenger-Versionen erkennen kann, falls Abweichungen bestehen. Üblicherweise versuchen Optimierer, die statistische Power-Marke von 80 % zu erreichen, denn je höher diese Kennzahl ist, desto geringer ist die Wahrscheinlichkeit, Fehler zweiter Art zu begehen.

Die statistische Aussagekraft nimmt einen Wert zwischen 0 und 1 an (und wird oft in %) ausgedrückt und steuert die Wahrscheinlichkeit Ihres Typ-II-Fehlers (β); er wird wie folgt berechnet: 1 – β

Je höher die statistische Aussagekraft Ihres Tests ist, desto geringer ist die Wahrscheinlichkeit, auf Fehler 2. Art zu stoßen.

Wenn also ein Experiment eine statistische Aussagekraft von 10 % hat, dann kann es ziemlich anfällig für einen Typ-II-Fehler sein. Wenn ein Experiment hingegen eine statistische Aussagekraft von 80 % hat, ist die Wahrscheinlichkeit eines Fehlers 2. Art weitaus geringer.

Erneut führen Sie Ihren Test durch, aber dieses Mal bemerken Sie keine signifikante Steigerung Ihrer Formularausfüllungen. Beide Versionen melden nahezu ähnliche Conversions. Aus diesem Grund brechen Sie Ihr Experiment ab und fahren mit der Originalversion ohne den Haftungsausschluss für die Einhaltung der DSGVO fort.

Wenn Sie sich jedoch eingehender mit Ihren Lead-Daten aus dem Testzeitraum befassen, stellen Sie fest, dass die Anzahl der Leads aus beiden Versionen (dem Original und dem Herausforderer) zwar identisch zu sein schien, die DSGVO-Version Ihnen jedoch einen guten, signifikanten Anstieg der Anzahl bescherte von Leads aus Europa. (Natürlich hätten Sie das Experiment mithilfe von Zielgruppen-Targeting nur den Leads aus Europa zeigen können – aber das ist eine andere Geschichte.)

Was hier passiert ist, ist, dass Sie Ihren Test zu früh beendet haben, ohne zu überprüfen, ob Sie genügend Leistung erreicht haben – und einen Typ-II-Fehler gemacht haben.

Vermeidung von Fehlern 2. Art in Ihren Experimenten

Führen Sie Tests mit hoher statistischer Aussagekraft durch, um Fehler vom Typ II zu vermeiden. Versuchen Sie, Ihre Experimente so zu konfigurieren, dass Sie mindestens die statistische Power-Marke von 80 % erreichen. Dies ist ein akzeptables Maß an statistischer Aussagekraft für die meisten Optimierungsexperimente. Damit stellen Sie sicher, dass Sie in mindestens 80 % der Fälle eine falsche Nullhypothese korrekt verwerfen.

Dazu müssen Sie sich die Faktoren ansehen, die dazu beitragen.

Die größte davon ist die Stichprobengröße (bei einer beobachteten Effektgröße). Die Stichprobengröße hängt direkt mit der Aussagekraft eines Tests zusammen. Eine große Stichprobengröße bedeutet einen Hochleistungstest. Tests mit zu geringer Leistung sind sehr anfällig für Typ-II-Fehler, da Ihre Chancen, Unterschiede in den Ergebnissen Ihrer Herausforderer- und Originalversionen zu erkennen, stark sinken, insbesondere bei niedrigen MEIs (mehr dazu weiter unten). Um Fehler vom Typ II zu vermeiden, warten Sie also, bis der Test genügend Leistung gesammelt hat, um Fehler vom Typ II zu minimieren. Idealerweise möchten Sie in den meisten Fällen eine Leistung von mindestens 80 % erreichen.

Ein weiterer Faktor ist der Minimum Effect of Interest (MEI) , den Sie für Ihr Experiment anstreben. MEI (auch MDE genannt) ist die Mindestgröße des Unterschieds, den Sie in Ihrem betreffenden KPI erkennen möchten. Wenn Sie einen niedrigen MEI festlegen (z. B. eine Erhöhung um 1,5 %), steigt Ihre Wahrscheinlichkeit, auf einen Fehler 2. Art zu stoßen, da die Erkennung kleiner Unterschiede wesentlich größere Stichprobenumfänge erfordert (um eine ausreichende Trennschärfe zu erreichen).

Und schließlich ist es wichtig zu beachten, dass es tendenziell eine umgekehrte Beziehung zwischen der Wahrscheinlichkeit, einen Fehler 1. Art zu machen (α) und der Wahrscheinlichkeit, einen Fehler 2. Art (β) zu machen, gibt. Wenn Sie beispielsweise den Wert von α verringern, um die Wahrscheinlichkeit eines Fehlers erster Art zu verringern (sagen wir, Sie setzen α auf 1 %, was ein Konfidenzniveau von 99 % bedeutet), wird die statistische Aussagekraft Ihres Experiments (oder seine Fähigkeit, β , einen Unterschied zu erkennen, wenn er vorhanden ist) verringert sich letztendlich auch, wodurch sich Ihre Wahrscheinlichkeit erhöht, einen Fehler 2. Art zu bekommen.

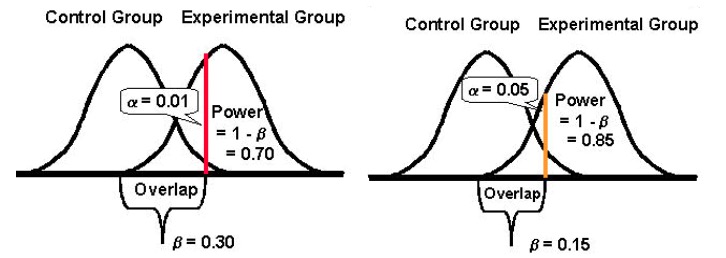
Einen der beiden Fehler besser akzeptieren: Typ I und II (und ein Gleichgewicht finden)

Die Verringerung der Wahrscheinlichkeit einer Fehlerart erhöht die der anderen Art (vorausgesetzt, alles andere bleibt gleich).

Sie müssen also den Anruf annehmen, welcher Fehlerart gegenüber Sie toleranter sein könnten.

Einerseits einen Typ-I-Fehler zu machen und eine Änderung für alle Ihre Benutzer einzuführen, könnte Sie Conversions und Einnahmen kosten – schlimmer noch, könnte auch ein Conversion-Killer sein.

Wenn Sie andererseits einen Fehler 2. Art begehen und es versäumen, eine erfolgreiche Version für alle Ihre Benutzer bereitzustellen, könnten Sie wiederum die Conversions kosten, die Sie andernfalls hätten gewinnen können.

Beide Fehler haben ausnahmslos ihren Preis.

Abhängig von Ihrem Experiment könnte jedoch eines für Sie akzeptabler sein als das andere. Im Allgemeinen empfinden Tester den Fehler 1. Art als etwa viermal schwerwiegender als den Fehler 2. Art .

Wenn Sie einen ausgewogeneren Ansatz wählen möchten, schlägt der Statistiker Jacob Cohen vor, dass Sie sich für eine statistische Aussagekraft von 80 % entscheiden sollten, die mit „ einem vernünftigen Gleichgewicht zwischen Alpha- und Beta-Risiko“ einhergeht. “ (80 % Leistung ist auch der Standard für die meisten Testwerkzeuge.)

Und was die statistische Signifikanz angeht, liegt der Standard bei 95 %.

Im Grunde dreht sich alles um Kompromisse und das Risiko, das Sie bereit sind zu tolerieren. Wenn Sie die Wahrscheinlichkeit beider Fehler wirklich minimieren möchten, können Sie ein Konfidenzniveau von 99 % und eine Leistung von 99 % wählen. Aber das würde bedeuten, dass Sie mit unglaublich großen Stichprobenumfängen für Zeiträume arbeiten würden, die ewig lang erscheinen. Außerdem würden Sie selbst dann Spielraum für Fehler lassen.

Hin und wieder WERDEN Sie ein Experiment falsch abschließen. Aber das ist Teil des Testprozesses – es dauert eine Weile, A/B-Teststatistiken zu beherrschen. Das Untersuchen und erneute Testen oder Nachverfolgen Ihrer erfolgreichen oder fehlgeschlagenen Experimente ist eine Möglichkeit, Ihre Ergebnisse zu bestätigen oder festzustellen, dass Sie einen Fehler gemacht haben.