Single Neuron Neuronales Netzwerk auf Python – mit mathematischer Intuition

Veröffentlicht: 2021-06-21

Lassen Sie uns ein einfaches Netzwerk aufbauen – sehr, sehr einfach, aber ein vollständiges Netzwerk – mit einer einzigen Schicht. Nur ein Input – und ein Neuron (das auch der Output ist), ein Gewicht, ein Bias.

Lassen Sie uns zuerst den Code ausführen und dann Teil für Teil analysieren

Klonen Sie das Github-Projekt oder führen Sie einfach den folgenden Code in Ihrer bevorzugten IDE aus.

Wenn Sie Hilfe beim Einrichten einer IDE benötigen, habe ich den Vorgang hier beschrieben.

Wenn alles in Ordnung ist, erhalten Sie diese Ausgabe:

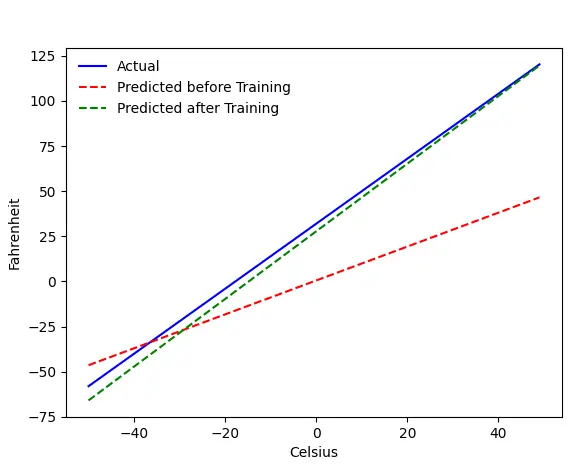
Das Problem – Fahrenheit von Celsius

Wir werden unsere Maschine trainieren, Fahrenheit aus Celsius vorherzusagen. Wie Sie dem Code (oder der Grafik) entnehmen können, ist die blaue Linie die tatsächliche Celsius-Fahrenheit-Beziehung. Die rote Linie ist die von unserer Babymaschine ohne Training vorhergesagte Beziehung. Schließlich trainieren wir die Maschine, und die grüne Linie ist die Vorhersage nach dem Training.

Schauen Sie sich Zeile 65–67 an – vor und nach dem Training wird mit derselben Funktion ( get_predicted_fahrenheit_values() ) vorhergesagt. Was also macht Magic Train()? Lass es uns herausfinden.

Netzwerkstruktur

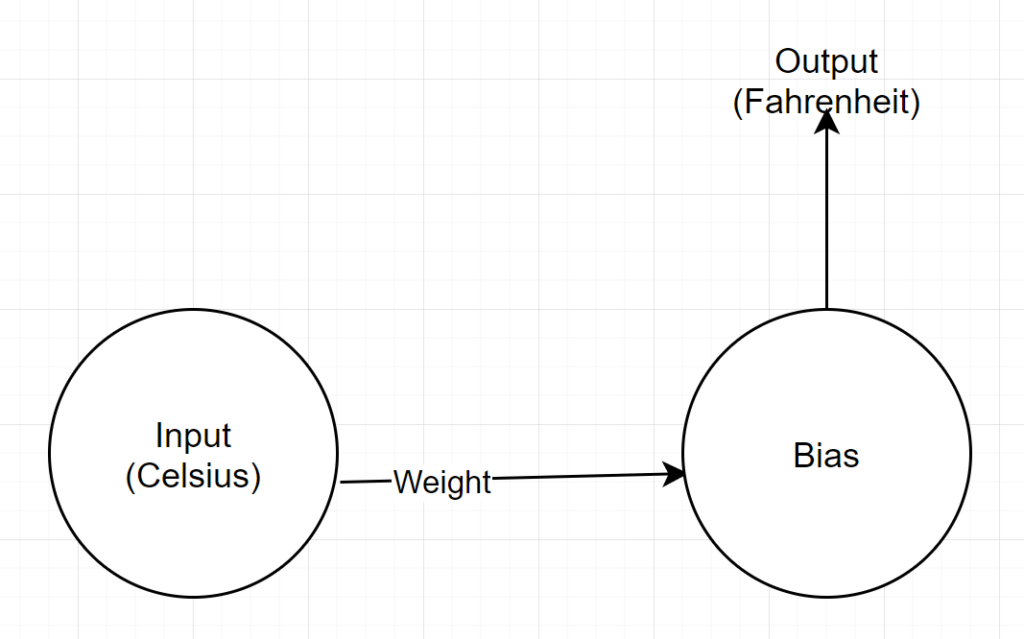
Eingabe: Eine Zahl, die Celsius darstellt

Gewicht: Ein Schwimmer, der das Gewicht darstellt

Bias: Ein Float, der den Bias darstellt

Ausgabe: Ein Float, der die vorhergesagte Fahrenheit darstellt

Wir haben also insgesamt 2 Parameter – 1 Gewicht und 1 Bias

Code-Analyse

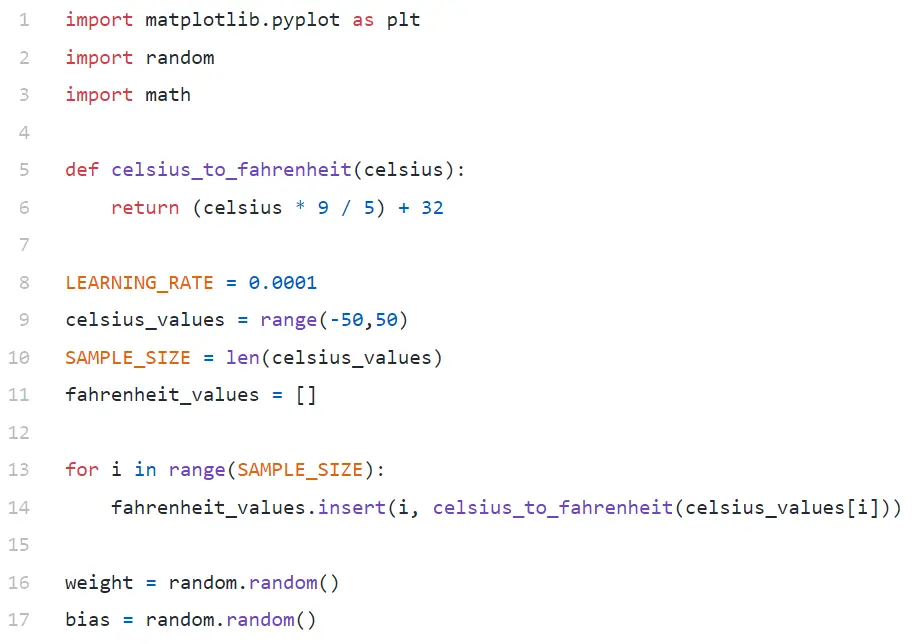
In Zeile 9 generieren wir ein Array aus 100 Zahlen zwischen -50 und +50 (ohne 50 – Bereichsfunktion schließt den oberen Grenzwert aus).

In Zeile 11–14 generieren wir die Fahrenheit für jeden Celsius-Wert.

In Zeile 16 und 17 initialisieren wir Gewichtung und Bias.

Zug()

Wir führen hier 10000 Trainingswiederholungen durch. Jede Iteration besteht aus:

vorwärts (Zeile #57) passieren
rückwärts (Zeile #58) passieren
update_parameters (Zeile #59)

Wenn Sie mit Python noch nicht vertraut sind, sieht es für Sie vielleicht etwas seltsam aus – Python-Funktionen können mehrere Werte als tuple zurückgeben.

Beachten Sie, dass update_parameters das einzige ist, woran wir interessiert sind. Alles andere, was wir hier tun, ist, die Parameter dieser Funktion auszuwerten, die die Gradienten (wir werden weiter unten erklären, was Gradienten sind) unserer Gewichtung und Vorspannung sind.

grad_weight: Ein Gleitkommawert, der den Gewichtsgradienten darstellt
grad_bias: Ein Gleitkommawert, der den Bias-Gradienten darstellt

Wir erhalten diese Werte, indem wir rückwärts aufrufen, aber es erfordert eine Ausgabe, die wir erhalten, indem wir in Zeile 57 vorwärts aufrufen.

nach vorne()

Beachten Sie, dass hier celsius_values und fahrenheit_values Arrays mit 100 Zeilen sind:

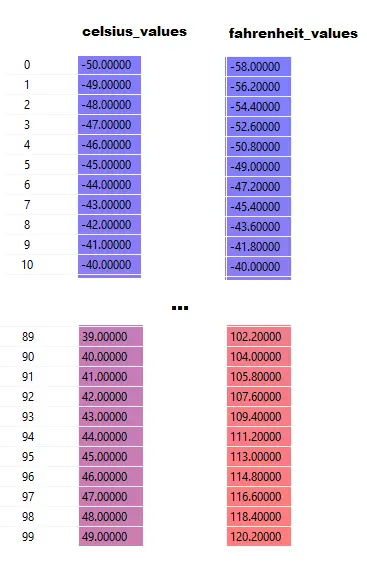
Sagen Sie nach dem Ausführen von Zeile 20–23 für einen Celsius-Wert 42

Ausgabe = 42 * Gewicht + Bias

Für 100 Elemente in celsius_values ist die Ausgabe also ein Array von 100 Elementen für jeden entsprechenden Celsius-Wert.

Zeile 25–30 berechnet den Verlust mithilfe der Verlustfunktion Mean Squared Error (MSE), die nur ein ausgefallener Name für das Quadrat aller Differenzen geteilt durch die Anzahl der Samples ist (in diesem Fall 100).

Kleiner Verlust bedeutet bessere Vorhersage. Wenn Sie den Druckverlust in jeder Iteration beibehalten, werden Sie feststellen, dass er mit fortschreitendem Training abnimmt.

Schließlich geben wir in Zeile 31 die vorhergesagte Ausgabe und den vorhergesagten Verlust zurück.

rückwärts

Wir sind nur daran interessiert, unsere Gewichtung und Neigung zu aktualisieren. Um diese Werte zu aktualisieren, müssen wir ihre Gradienten kennen, und die berechnen wir hier.

Beachten Sie, dass Gradienten in umgekehrter Reihenfolge berechnet werden. Der Gradient der Ausgabe wird zuerst berechnet und dann für Gewicht und Bias, daher der Name „Backpropagation“. Der Grund dafür ist, dass wir zur Berechnung des Gewichtungs- und Biasgradienten den Ausgabegradienten kennen müssen – damit wir ihn in der Kettenregelformel verwenden können.

Schauen wir uns nun an, was Gradient und Kettenregel sind.

Gradient

Stellen Sie sich der Einfachheit halber vor, dass wir nur einen Wert von celsius_values und fahrenheit_values haben, 42 bzw. 107,6 .

Nun lautet die Aufschlüsselung der Berechnung in Zeile 30:

Verlust = (107,6 — (42 * Gewicht + Bias))² / 1

Wie Sie sehen, hängt der Verlust von 2 Parametern ab – Gewichtungen und Bias. Betrachten Sie das Gewicht. Stellen Sie sich vor, wir haben es mit einem zufälligen Wert initialisiert, sagen wir 0,8, und nach Auswertung der obigen Gleichung erhalten wir 123,45 als Wert von loss . Basierend auf diesem Verlustwert müssen Sie entscheiden, wie Sie das Gewicht aktualisieren. Sollten Sie es 0,9 oder 0,7 machen?

Sie müssen das Gewicht so aktualisieren, dass Sie in der nächsten Iteration einen niedrigeren Wert für den Verlust erhalten (denken Sie daran, dass die Minimierung des Verlusts das ultimative Ziel ist). Wenn also zunehmendes Gewicht den Verlust erhöht, werden wir ihn verringern. Und wenn zunehmendes Gewicht den Verlust verringert, werden wir ihn erhöhen.

Nun stellt sich die Frage, woher wir wissen, ob zunehmendes Gewicht den Verlust erhöht oder verringert. Hier kommt der Gradient ins Spiel . Im Großen und Ganzen wird der Gradient durch die Ableitung definiert. Erinnern Sie sich an Ihren Schulkalkül, dass ∂y/∂x (das eine partielle Ableitung/ein Gradient von y in Bezug auf x ist) angibt, wie sich y bei einer kleinen Änderung von x ändern wird.

Wenn ∂y/∂x positiv ist, bedeutet dies, dass eine kleine Erhöhung von x y erhöht.

Wenn ∂y/∂x negativ ist, bedeutet dies, dass eine kleine Erhöhung von x y verringert.

Wenn ∂y/∂x groß ist, bewirkt eine kleine Änderung von x eine große Änderung von y.

Wenn ∂y/∂x klein ist, bewirkt eine kleine Änderung von x eine kleine Änderung von y.

Von Steigungen erhalten wir also 2 Informationen. In welche Richtung der Parameter aktualisiert werden muss (erhöhen oder verringern) und wie viel (groß oder klein).

Kettenregel

Informell gesprochen sagt die Kettenregel:

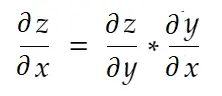
Betrachten Sie das obige Beispiel für das Gewicht . Wir müssen grad_weight berechnen, um dieses Gewicht zu aktualisieren, das berechnet wird durch:

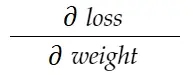
Mit der Kettenregelformel können wir es ableiten:

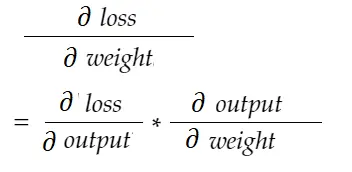
In ähnlicher Weise Gradient für Bias:

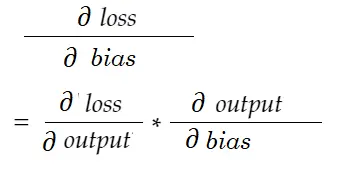
Lassen Sie uns ein Abhängigkeitsdiagramm zeichnen.

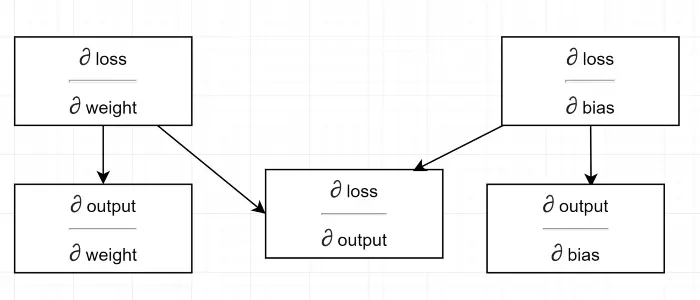
Siehe alle Berechnung hängt vom Gradienten der Leistung ab (∂ Verlust/∂ Leistung) . Deshalb berechnen wir es zuerst auf dem Backpass (Zeile #34–36).

Tatsächlich müssen Sie in High-Level-ML-Frameworks, zum Beispiel in PyTorch, keine Codes für Backpass schreiben! Während des Vorwärtsdurchlaufs erstellt es Berechnungsdiagramme, und während des Rückdurchlaufs geht es durch die entgegengesetzte Richtung im Diagramm und berechnet Gradienten unter Verwendung der Kettenregel.

∂ Verlust / ∂ Leistung

Wir definieren diese Variable durch grad_output im Code, den wir in Zeile 34–36 berechnet haben. Lassen Sie uns den Grund hinter der Formel herausfinden, die wir im Code verwendet haben.

Denken Sie daran, dass wir alle 100 celsius_values zusammen in die Maschine einspeisen. grad_output ist also ein Array aus 100 Elementen, wobei jedes Element den Ausgabegradienten für das entsprechende Element in celsius_values enthält . Nehmen wir der Einfachheit halber an, dass es in celsius_values nur 2 Elemente gibt.

Also, Zeile 30 aufschlüsseln,

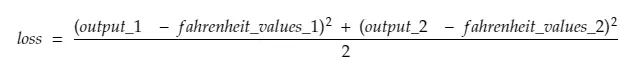
wo,

Ausgang_1 = Ausgangswert für 1. Celsiuswert

Ausgang_2 = Ausgangswert für 2. Celsiuswert

fahreinheit_values_1 = Aktueller Fahreinheitswert für 1. Grad Celsius

fahreinheit_values_1 = Aktueller Fahreinheitswert für 2. Grad Celsius

Nun enthält die resultierende Variable grad_output 2 Werte — Gradient von output_1 und output_2, was bedeutet:

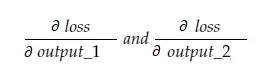
Lassen Sie uns nur den Gradienten von output_1 berechnen, und dann können wir die gleiche Regel für die anderen anwenden.

Rechenzeit!

Das ist dasselbe wie Zeile 34–36.

Gewichtsverlauf

Stellen Sie sich vor, wir haben nur ein Element in celsius_values. Jetzt:

Das ist dasselbe wie Zeile 38–40. Für 100 celsius_values werden Steigungswerte für jeden der Werte summiert. Eine naheliegende Frage wäre, warum wir das Ergebnis nicht verkleinern (dh durch SAMPLE_SIZE dividieren). Da wir vor dem Aktualisieren der Parameter alle Gradienten mit einem kleinen Faktor multiplizieren, ist dies nicht erforderlich (siehe letzten Abschnitt Parameter aktualisieren).

Neigungsgradient

Das ist dasselbe wie Line#42. Wie Gewichtungsgradienten werden diese Werte für jede der 100 Eingaben summiert. Auch hier ist es in Ordnung, da Gradienten mit einem kleinen Faktor multipliziert werden, bevor die Parameter aktualisiert werden.

Aktualisieren von Parametern

Schließlich aktualisieren wir die Parameter. Beachten Sie, dass die Gradienten mit einem kleinen Faktor (LEARNING_RATE) multipliziert werden, bevor sie subtrahiert werden, um das Training stabil zu machen. Ein großer Wert von LEARNING_RATE führt zu einem Überschreitungsproblem und ein extrem kleiner Wert verlangsamt das Training, was möglicherweise viel mehr Iterationen erfordert. Wir sollten mit etwas Trial-and-Error einen optimalen Wert dafür finden. Es gibt viele Online-Ressourcen, einschließlich dieser, um mehr über die Lernrate zu erfahren.

Beachten Sie, dass der genaue Betrag, den wir anpassen, nicht extrem kritisch ist. Wenn Sie beispielsweise LEARNING_RATE ein wenig optimieren, werden die Variablen descent_grad_weight und descent_grad_bias (Zeile Nr. 49–50) geändert, aber die Maschine funktioniert möglicherweise immer noch. Wichtig ist, dass diese Beträge abgeleitet werden, indem die Gradienten mit demselben Faktor (in diesem Fall LEARNING_RATE) herunterskaliert werden. Mit anderen Worten, „das Gefälle der Steigungen proportional zu halten“ ist wichtiger als „wie stark sie abfallen “.

Beachten Sie auch, dass diese Gradientenwerte eigentlich die Summe der Gradienten sind, die für jede der 100 Eingaben ausgewertet werden. Da diese aber mit dem gleichen Wert skaliert sind, ist es wie oben erwähnt in Ordnung.

Um die Parameter zu aktualisieren, müssen wir sie mit dem Schlüsselwort global deklarieren (in Zeile 47).

Wohin von hier aus

Der Code wäre viel kleiner, wenn die for-Schleifen durch Listenverständnis auf pythonische Weise ersetzt würden. Schauen Sie es sich jetzt an – es würde nicht länger als ein paar Minuten dauern, es zu verstehen.

Wenn Sie bisher alles verstanden haben, ist es wahrscheinlich an der Zeit, sich die Interna eines einfachen Netzwerks mit mehreren Neuronen/Schichten anzusehen – hier ist ein Artikel.