Normalverteilung – eine intuitive Einführung ohne Mathematik

Ich werde versuchen, diesen Artikel so weit wie möglich frei von Gleichungen und Fachjargon zu halten. Ich benötige jedoch mindestens die folgenden Fähigkeiten:

• Kann einfache Grafiken interpretieren.
• Grundlegende Kenntnisse in Wahrscheinlichkeit. Du verstehst wenigstens, dass es eine 50%ige Wahrscheinlichkeit für den Kopf gibt, wenn ich eine Münze werfe.
• Integralrechnung und Quantenphysik (Scherz!)

Warum Normalverteilung

Ein intuitiver Weg, etwas zu verstehen, besteht darin, zu untersuchen, warum es benötigt wird. Machen wir es für die Normalverteilung (auch Gaußsche Verteilung genannt).

Angenommen, Sie haben eine lustige Angewohnheit. Jeden Tag wirfst du 100 Mal eine Münze. Es ist „normal“, zu erwarten, dass Sie 50 Mal Kopf bekommen – oder fast 50 Mal den größten Teil des Tages. Selten gibt es gute Tage für den Kopf – Sie können etwa 55 Mal und sehr selten mehr als 65 Mal erreichen.

Nun wollen Sie diese „Seltenheit“ quantifizieren. Also fängst du an zu verfolgen, wie oft du jeden Tag den Kopf bekommen hast.

Anzahl der Köpfe pro Tag in einem Jahr

Unten sind die Daten nach einem Jahr (365 Tage) – der erste ist die Anzahl der Köpfe, die Sie am ersten Tag erhalten haben, und der letzte ist die Anzahl der Köpfe, die Sie am letzten Tag erhalten haben. Sie müssen nicht alle Zahlen unten überprüfen, aber es ist leicht zu erkennen, dass die meisten um die 50 liegen.

56, 47, 54, 50, 57, 51, 57, 48, 54, 62, 42, 51, 37, 42, 50, 37, 59, 48, 46, 51, 61, 47, 46, 48, 63, 55, 50, 50, 43, 46, 56, 49, 50, 54, 52, 47, 51, 59, 61, 53, 44, 53, 59, 58, 54, 54, 50, 49, 51, 46, 43, 51, 49, 54, 46, 44, 41, 51, 51, 49, 64, 46, 46, 46, 52, 48, 57, 49, 42, 46, 55, 50, 52, 51, 47, 53, 50, 48, 58, 43, 60, 49, 46, 42, 53, 45, 57, 48, 52, 47, 47, 47, 42, 57, 60, 49, 48, 50, 51, 47, 48, 52, 47, 45, 51, 55, 51, 45, 46, 46, 40, 52, 57, 48, 51, 48, 44, 46, 41, 59, 60, 46, 44, 36, 48, 52, 49, 49, 49, 51, 41, 49, 51, 51, 42, 51, 45, 54, 50, 48, 49, 43, 52, 53, 52, 53, 48, 37, 53, 54, 41, 48, 52, 46, 47, 57, 50, 49, 46, 57, 67, 50, 54, 48, 50, 60, 43, 49, 57, 57, 45, 55, 57, 52, 46, 48, 49, 51, 45, 48, 44, 48, 55, 51, 59, 52, 50, 55, 51, 46, 48, 51, 46, 50, 49, 50, 47, 51, 43, 46, 48, 56, 47, 57, 44, 54, 52, 55, 46, 49, 53, 40, 54, 54, 49, 50, 53, 41, 55, 50, 42, 58, 47, 53, 55, 45, 52, 61, 50, 49, 48, 51, 50, 56, 44, 47, 45, 48, 63, 43, 52, 55, 46, 48, 52, 49, 56, 62, 57, 54, 47, 51, 52, 43, 45, 57, 51, 46, 42, 52, 57, 54, 48, 54, 51, 49, 51, 42, 52, 50, 52, 61, 61, 44, 45, 48, 49, 48, 46, 47, 57, 44, 44, 47, 52, 47, 42, 48, 51, 58, 36, 57, 53, 49, 52, 50, 52, 56, 44, 56, 46, 42, 46, 43, 56, 49, 44, 38, 46, 52, 49, 58, 51, 49, 48, 52, 57, 43, 48, 40, 52, 54, 40, 54, 45, 49, 41, 57, 50, 52, 43, 54, 49, 45, 44, 53, 49, 43, 51, 50, 56, 45, 46, 47, 41, 52, 59, 52, 50, 48, 58, 52, 51, 55, 49, 41, 38, 57, 56, 41, 54, 44, 47, 60, 44

Besser visualisieren mit Histogramm

Lassen Sie uns ein Histogramm aus den obigen Daten zeichnen:

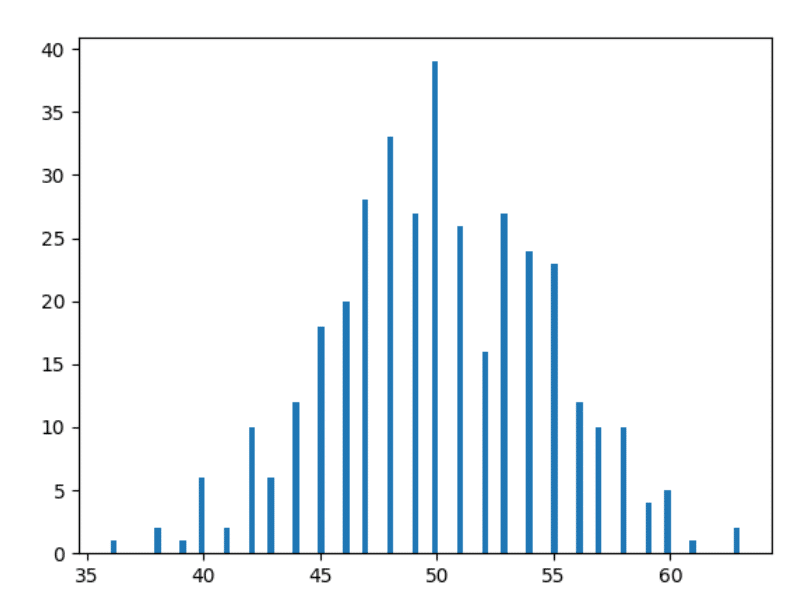
Aha! Sieht es nicht schon so aus wie das Bild, das Sie im Internet gesehen haben, als Sie „Normalverteilung“ gegoogelt haben? Wir sind fast da!

Also, wenn Sie Histogramme nicht verstehen – wir haben hier nur die Anzahl der Tage aufgetragen, an denen wir eine bestimmte Zählung für den Kopf erhalten haben. Zum Beispiel haben wir 36 Mal an 2 bestimmten Tagen im Jahr Kopf bekommen (überprüfen Sie die Daten oben, wenn Sie mir nicht glauben), deshalb gibt es einen Balken mit einer Höhe von 2 Einheiten auf dem horizontalen Punkt bei 36 (der rote Rechteck links im Bild unten).

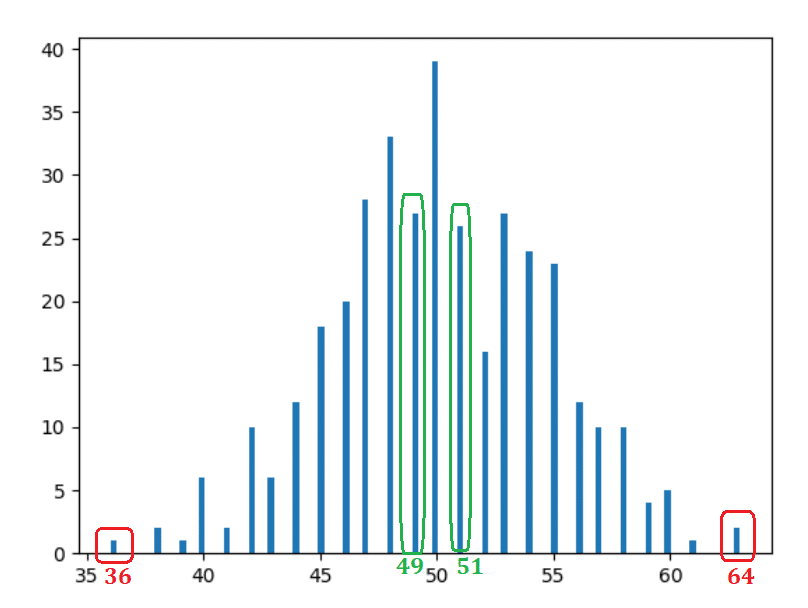
Beobachtungen

1. Ziemlich offensichtlich und erwartet – 50 Köpfe traten die meiste Zeit auf.
2. Je weiter wir uns vom Zentrum (50) entfernen, desto mehr nimmt das Vorkommen ab.
3. Stäbe im gleichen Abstand nehmen ähnliche Formen an. Wenn Sie beispielsweise eine Einheit nach links (49) oder rechts (51) verschieben, sind die Vorkommnisse ähnlich – 30 bzw. 31 (die grünen Rechtecke). Wenn Sie sich 14 Einheiten nach links (36) oder rechts (64) bewegen, sind die Vorkommnisse wieder ähnlich – 2 bzw. 1 (rote Rechtecke).

10 Jahre Daten

Lassen Sie uns jetzt ein wenig vorspulen – und die Daten von 10 Jahren darstellen.

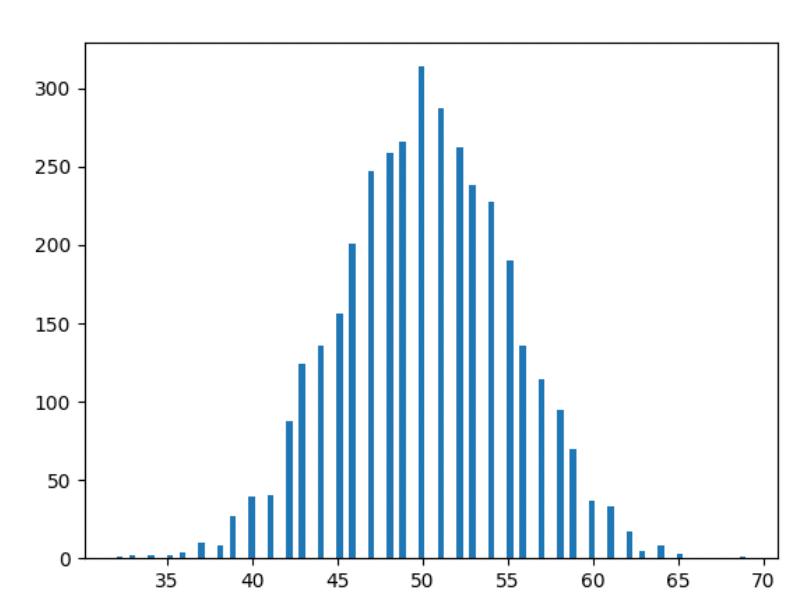
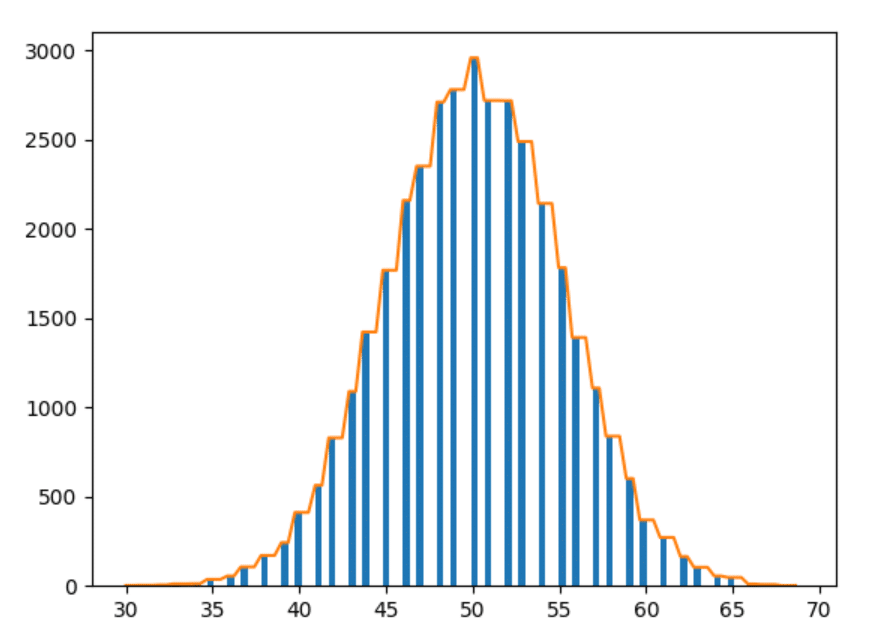
1000 Jahre Daten

Okay – das Letzte. Lassen Sie uns die Daten von 1000 Jahren darstellen.

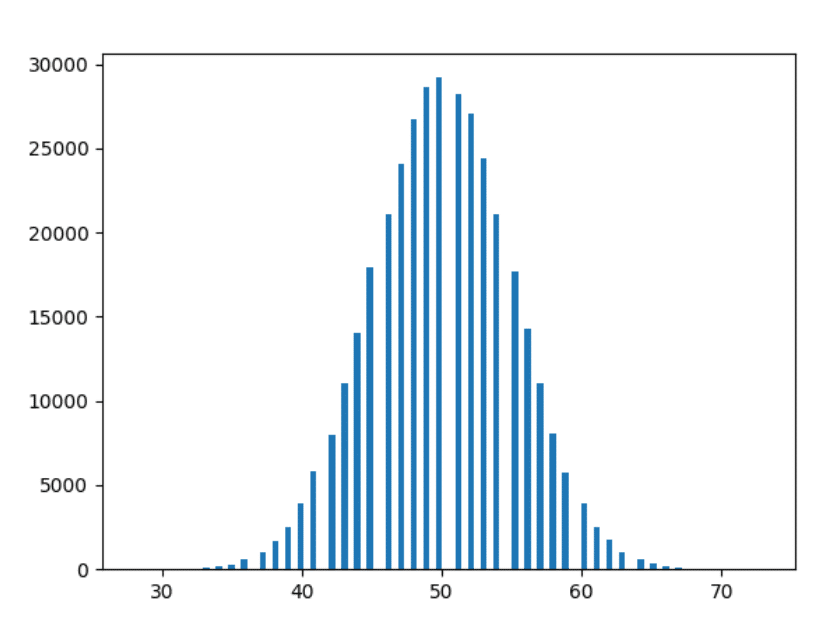
Beobachtungen

1. Je mehr wir experimentieren, desto glatter werden die Formen.
2. Je mehr wir experimentieren, desto mehr folgen die Balken den obigen Beobachtungen (dh Balken in ähnlichem Abstand nehmen engere Formen an).

Wo ist die verdammte Normalverteilung?

Okay – zu viel Hintergrund – jetzt kommen wir zum Punkt.

Sehen wir uns die von Google vorgeschlagene Antwort an:

Ein paar Dinge in dieser Definition:

Zufallsvariable: Einfach ausgedrückt – eine Zufallsvariable ist eine Menge möglicher Werte eines Zufallsexperiments wie ein Münzwurf. In unserem Beispiel ist der mögliche Wert unseres Experiments Head oder Tail .

Glockenförmig : Haben Sie bemerkt, dass unser Histogramm eine Glockenform annimmt?

Symmetrisch: Balken im gleichen Abstand haben ähnliche Formen – ist das nicht symmetrisch?

Die Normalverteilung stellt also die Verteilung der Ergebnisse für Ereignisse wie Münzwurf dar – wobei die Verteilung dazu neigt, einige Eigenschaften beizubehalten, einschließlich der Symmetrie und der Glockenform.

Welche anderen Phänomene als der Münzwurf folgen der Normalverteilung?

Einige coole Beispiele hier.

• Größe in der Bevölkerung – mehr Menschen fallen in die Gruppe der durchschnittlichen Größe. Es ist selten, extrem große oder extrem kleine Menschen zu finden. Und die Chancen, extrem groß und extrem klein zu finden, sind fast gleich.
• Würfeln
• Schuhgröße
• IQ
• Und vieles andere …

Folgen diese Phänomene strikt der Normalverteilung?

Die einfache Antwort ist nein. Obwohl, wie wir oben gesehen haben, je mehr Sie experimentieren, desto mehr folgen die Daten den Eigenschaften der Normalverteilung. Aber es gibt keine Gewissheit, dass nicht trotzdem ein unwahrscheinliches Ereignis eintritt.

Sind alle Wahrscheinlichkeitsverteilungen im Universum normalverteilt?

Nein. Es gibt viele Phänomene, die durch eine andere Art der Verteilung bestimmt werden.

• Die Wahrscheinlichkeit, dass eine bestimmte Anzahl von Kunden ankommt, telefoniert, Unfälle, Sportereignisse und Überschwemmungen auftreten, folgt der Poisson-Verteilung .
• Beim Geschäftsverkauf sind 20 % der Kunden eines Unternehmens für 80 % des Umsatzes verantwortlich. ( Pareto-Verteilung )
• Verkehrsmuster in einer Stadt – Exponentialverteilung
• Zufällige Auswahl von Mitgliedern für ein Team aus einer Population von Mädchen und Jungen – hypergeometrische Verteilung

Und viele mehr …

Ich habe die obige Liste erstellt, indem ich einfach „Beispiel aus dem wirklichen Leben“ mit einigen hier aufgeführten Distributionen gegoogelt habe – nicht, dass ich sie alle verstehe. 😉

Gibt es einen Grund, warum einige Naturphänomene dazu neigen, einer Normalverteilung zu folgen?

Ja – ich zitiere meine Lieblingserklärung:

Die übliche Erklärung wird durch einen anderen Namen für die Normalverteilung gegeben, nämlich die „Fehlerverteilung“. Die Idee ist, dass Fehler im Allgemeinen zufällig sind, so dass sie genauso wahrscheinlich in die eine wie in die andere Richtung gehen. Zum Beispiel schießt der Schütze genauso wahrscheinlich ein bisschen nach links, wie ein bisschen nach rechts oder ein bisschen hoch wie ein bisschen tief. Daher spiegelt ein Diagramm, wie weit die Schüsse vom Bullseye entfernt sind, diese zufällige Tendenz wider und ist symmetrisch um den Mittelwert. In ähnlicher Weise tragen bei Größe und Intelligenz viele Gene (vielleicht Tausende) zu diesen Ergebnissen bei, ebenso wie eine große Anzahl von Umweltfaktoren wie Ernährung, Krankheiten, niedriges Einkommen und so weiter.

Parameter der Normalverteilung

Wenn Sie bisher eine Ahnung von der Diskussion haben, sind Sie bereits der Gewinner. Mission erfüllt. Der Rest des Artikels ist ein Bonus.

Alle Normalverteilungsgraphen, die Sie sehen, haben unterschiedliche Formen. Einige von ihnen sind flacher als andere. Einige von ihnen haben gute Höhen. Alle diese Formen werden von nur 2 Parametern gesteuert:

Gemein

Der Mittelwert wird durch den Durchschnitt definiert. Sie definiert die Höhe der Glocke. Für das Beispiel des Münzwurfs liegt der Mittelwert nahe bei 50, was der obersten Position in der Grafik entspricht.

Standardabweichung

Da ich verspreche, dass dieser Artikel frei von Gleichungen sein wird, gebe ich hier keine mathematische Darstellung. Aber es ist sowieso nicht so schwer. Die Standardabweichung ist eine Metrik, die darstellt, wie vielfältig die Daten sind.

Beispielsweise wird die Standardabweichung des Alters in der Kinderbetreuung geringer sein als die Standardabweichung des Alters im Fußball-Fanclub, da der Altersunterschied zwischen der jüngsten und der ältesten Gruppe im Fußball-Fanclub viel größer sein sollte.

Die Standardabweichung bestimmt die Breite der Kurve. Eine kleine Standardabweichung erzeugt eine steile Kurve, und eine größere Standardabweichung erzeugt eine flachere Kurve.