Fühlen Sie Kalkül mit Ihrem Programmiersinn

Ich glaube, dass Leute, die programmieren können, die Fähigkeit haben, kompliziertere Konzepte als Kalkül zu verstehen. Ein Grund, warum es viele talentierte Programmierer gibt, die immer noch mit Kalkül zu kämpfen haben, ist nicht, dass es schwierig ist. Es liegt hauptsächlich daran, dass es uns falsch beigebracht wurde (zusammen mit vielen anderen Themen).

Wenn Sie in Ihrem Leben etwas codiert haben – sogar einige Spielzeugübungen wie das Generieren von Primzahlen –, haben Sie vielleicht bereits ähnliche Dinge getan, die in der Analysis passieren, aber nie die Gelegenheit gehabt, sich darauf zu beziehen.

Das Ziel dieses Artikels ist weder, Ihnen Kalkül noch Programmieren beizubringen, sondern Ihnen zu helfen, einige Punkte zu verbinden.

Ich werde in einer Minute zum Codierungsteil kommen. Aber gestatten Sie mir, vorher einige kurze Hintergrundinformationen zu geben.

Änderungsrate

Die Differentialrechnung spricht von der „Änderungsrate“. Versuchen wir zu verstehen, was das bedeutet.

Bei einer Änderung einer Variablen (x) ist die Änderungsrate einer Funktion einfach die Änderung der Funktion dividiert durch die Änderung von x. Lassen Sie sich mit tatsächlichen Zahlen visualisieren:

Betrachten Sie 2 Punkte x=2 und x=6 und eine Funktion y=f(x) = x².

Betrachten Sie auch dx = Abstand zwischen diesen 2 Punkten auf der x-Achse. Und dy ist der Abstand zwischen y-Werten für diese x-Werte.

Dann ist die Änderungsrate in y von x = 2 bis x = 6

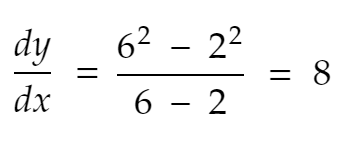
Derivat

Nun ist die Ableitung dy/dx die Änderungsrate von y für eine infinitesimal kleine Änderung von x. Da dieser Abstand (6–2=4) nicht unendlich klein ist – nicht einmal annähernd, können wir die obige Gleichung nicht als Ableitung bezeichnen. Wählen wir also vorerst eine kleinere Zahl, 0,1 .

Wenn x = 0, y = x² = 0² = 0.

Nächster Nachbar in positiver Richtung, x = 0,1. Dort wird y zu 0,1² = 0,01.

So,

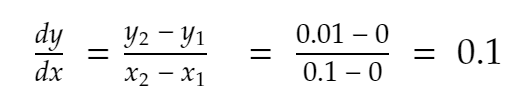
Versuchen wir es noch einmal. Nächster Nachbar von 0,1 in positiver Richtung, x = 0,2. Also wird y zu 0,2² = 0,04. So,

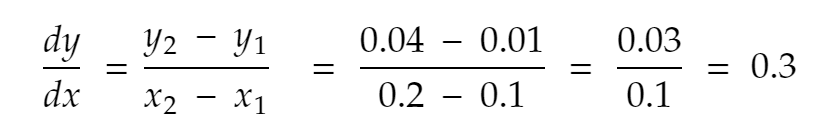
Wenn wir den Vorgang noch ein paar Mal wiederholen, erhalten wir Folgendes:

Hier ist die Excel-Datei, wenn Sie damit spielen möchten.

dx (das ist unser fiktiver infinitesimal kleiner Abstand zwischen 2 benachbarten Punkten auf der x-Achse) ist in unserem Kontext 0,1.

x nimmt entsprechend zu.

y ist einfach x².

dy ist der Abstand zwischen zwei benachbarten y-Werten. Wenn beispielsweise x = 0,1 ist, beträgt der Abstand zwischen dem aktuellen y (0,01 ) und dem nächsten y (0,04) 0,03 – also ist dy 0,03 bei x = 0,1.

dy/dx ist dy dividiert durch dx.

dy/dx / x ist dy/dx dividiert durch x.

Beachten Sie nun, dass sich die letzte Zeile mit zunehmendem x dem Wert 2 nähert, was bedeutet, dass sich die Änderungsrate von x² in Bezug auf x dem Doppelten von x nähert, was 2x entspricht.

Erinnern Sie sich an die Ableitung von x² nach x? 2x! Verbindung finden?

Codierzeit

Lassen Sie uns die Dinge im Code ausprobieren, die wir bisher besprochen haben.

Angenommen, Sie haben Python bereits installiert, führen Sie im Terminal Folgendes aus:

Führen Sie danach den folgenden Python-Code aus:

Hier:

x : Enthält Zahlen von 0 bis 9.

y : ein weiteres Array, jedes Element ist ein Quadrat des entsprechenden x-Elements

dy : Ein weiteres Array, das mit Nullen initialisiert wurde. Wir werden y-Abstände in dieses Array einfügen.

dydx : Ein weiteres Array, das mit Nullen initialisiert wurde. Es enthält den dy/dx-Wert jedes Punktes.

dx : Ziemlich offensichtlich – es ist die Schrittweite. Abstand zwischen 2 aufeinanderfolgenden Zahlen, der mit zunehmender SIZE abnimmt. Wenn SIZE = 10, dx = 1. Wenn SIZE = 100, dx = 0,1.

Zuerst leiten wir dy für jeden Punkt ab. Dann berechnen wir daraus dydx.

Beachte das:

Hier lassen wir den ersten und den letzten Wert weg. Der erste Wert von x ist 0, was einen Nullteilungsfehler erzeugt. Und wir können den letzten Wert von dy/dx nicht berechnen, da wir den letzten Wert von dy nicht haben – weil es den letzten verfügbaren Wert von y erfordern würde, den wir hier nicht haben.

Wenn alles gut geht, erhalten Sie diese Grafik:

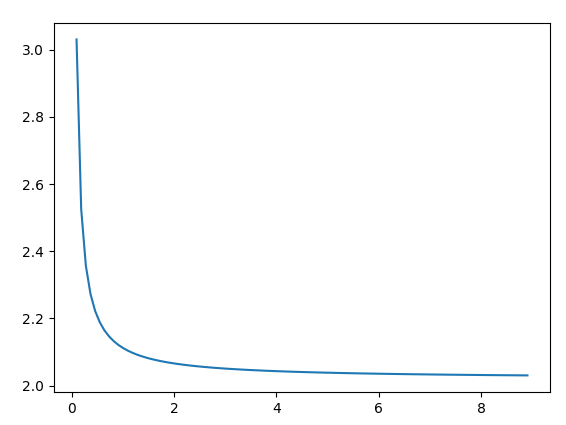
Was Sie aus der Handlung verstehen

Wie Sie sehen, nähert sich der Graph 2. Erhöhen Sie den Wert von SIZE (was bedeutet, dass Sie dx auf einen niedrigeren Wert setzen) und sehen Sie, wie sich der Graph schneller 2 nähert.

Zweite Ableitung

Jetzt, wo Sie so weit gekommen sind, brauchen Sie nur noch ein paar Schritte, um die zweite Ableitung zu realisieren, die Ihnen die Intuition für die Ableitung jeder Ordnung geben wird.

Wie Sie sich erinnern, ist die zweite Ableitung die Änderungsrate der ersten Ableitung in Bezug auf x. Einfach ausgedrückt – dy/dx in der zweiten Ableitung ist wie y in der ersten Ableitung.

Nehmen wir die folgenden Änderungen am obigen Code vor:

Deklarieren Sie 2 weitere Arrays:

d2ydx2 : Was die zweite Ableitung darstellt:

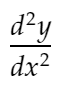
distance_dydx: Zur Darstellung des Abstands zwischen dy/dx-Werten zwischen 2 benachbarten Punkten

Hier ist der vollständige Code für die zweite Ableitung:

Nach der Berechnung von dydx in der for-Schleife führen wir eine weitere Schleife aus, um die zweite Ableitung zu berechnen. Mit etwas kluger Codierung könnten wir die zweite Ableitung in derselben Schleife berechnen (versuchen Sie es als Übung) – aber ich habe sie hier der Übersichtlichkeit halber getrennt.

Beachten Sie auch Folgendes:

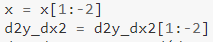
Wie bei der ersten Ableitung lassen wir auch hier einige Werte weg. Die letzten 2 Werte werden weggelassen, da der vorletzte den letzten Wert der „ersten Ableitung“ erfordern würde, den wir nicht berechnen könnten (da wir den erforderlichen y-Wert dafür nicht hatten – wie oben beschrieben). Bedeutet das, dass wir bei der 3. Ableitung die letzten 3 Werte weglassen müssen?🤔 — das musst du selbst herausfinden.

Hier ist das Ausgabediagramm:

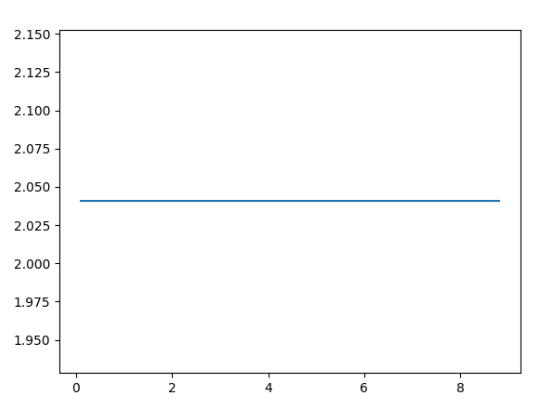
Was sehen wir hier?

Wie man es von der Oberstufe kennt:

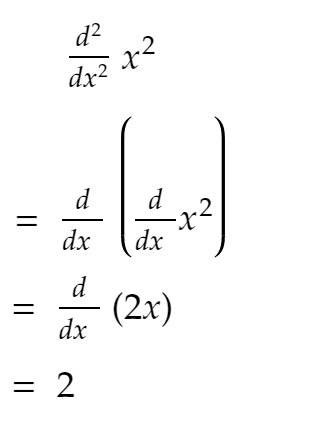
Wie Sie dem obigen Code entnehmen können, bleibt die zweite Ableitung größtenteils konstant, und wenn Sie SIZE weiter erhöhen, nähert sie sich 2!

Warum die Änderungsrate wichtig ist

Sie fragen sich vielleicht:

— Warum überstehen wir all diese unangenehmen Probleme? Welche nützlichen Informationen erhalten wir aus der Änderungsrate oder der Ableitung?

— Warum können wir nicht einfach mit der Änderungsrate für jeden Betrag gehen? Warum nur verschwindend klein? Welche Informationen erhalten wir aus der Änderungsrate in Bezug auf infinitesimal kleine Werte, die wir nicht aus der Änderungsrate in Bezug auf größere Werte finden können?

— Dieses winzig kleine Ding sieht aus wie ein Hack? Wir haben mit einigen kleinen Zahlen oben in Ordnung gearbeitet – aber sicherlich nicht wirklich unendlich klein.

Wenn ich mir erlaube, weiterzumachen, würden Sie weggehen, wenn Sie die Länge dieses Artikels sehen würden, und wären nicht so weit gekommen. Vielleicht werden wir diese Fragen an einem anderen Tag ansprechen 😀.