Bayes'sche Statistik: Eine schnelle und hypefreie Einführung für A/B-Tester
Veröffentlicht: 2022-06-23
Wie sicher sind Sie in Ihrer Fähigkeit, die Ergebnisse Ihres A/B-Testing-Tools zu interpretieren?
Angenommen, Sie verwenden ein Tool, das auf Bayes-Statistiken basiert, und es hat Ihnen mitgeteilt, dass „B“ eine 70-prozentige Chance hat, „A“ zu schlagen, also ist „B“ der Gewinner. Wissen Sie, was das bedeutet und wie es Ihre CRO-Strategie beeinflussen sollte?
In diesem Artikel lernen Sie die Grundlagen der Bayes'schen Statistik kennen, die Ihnen dabei helfen, die Kontrolle über Ihre A/B-Tests zurückzugewinnen, einschließlich
- Ein unvoreingenommener Blick auf die Bayes'sche Statistik
- Vor- und Nachteile von Frequentisten vs. Bayesianern
- Die Vorbereitung, die Sie benötigen, um Bayes'sche A/B-Testergebnisse sicher zu interpretieren und zu verwenden und gleichzeitig einige gängige Mythenfallen zu vermeiden.
- Was ist Bayessche Statistik?
- Die Bayes'sche Ursprungsgeschichte
- Ein Beispiel für Bayes'sche Statistik, die auf A/B-Tests angewendet wird
- Ein kurzes Glossar Bayes'scher Begriffe, die für A/B-Tester wichtig sind
- Bayessche Inferenz
- Bedingte Wahrscheinlichkeit
- Wahrscheinlichkeitsverteilung/Wahrscheinlichkeitsverteilung
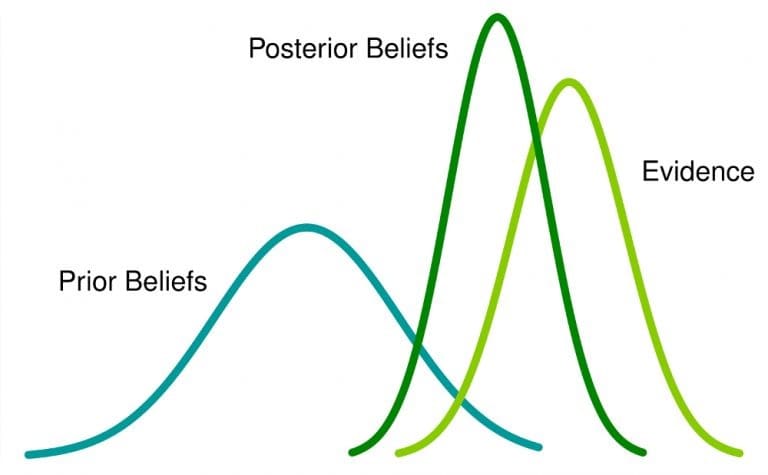
- Verteilung der vorherigen Überzeugungen
- Konjugation
- Prioren konjugieren
- Verlustfunktion
- Was ist Frequentistische Statistik?
- Bayesianisches vs. Frequentistisches A/B-Testen
- Das Frequentistische Framework
- Das Bayessche Framework
- Was sagt Ihnen die Bayes'sche Statistik eigentlich beim A/B-Testen?
- Wahrscheinlichkeit, der Beste zu sein (P2BB)
- Erwarteter Aufstieg
- Erwarteter Verlust
- Mythen rund um die Bayes'sche Statistik, die es zu vermeiden gilt
- Mythos Nr. 1: Bayesianer formulieren ihre Annahmen, Frequentisten nicht
- Mythos Nr. 2. Bayesianische Methoden geben Ihnen die Antworten, die Sie wirklich wollen
- Mythos Nr. 3: Bayes'sche Inferenz hilft Ihnen, Unsicherheit besser zu kommunizieren als häufige Inferenz
- Mythos Nr. 4. Bayes'sche A/B-Testergebnisse sind immun gegen Peeking
- Mythos Nr. 5. Frequentistische Statistiken sind ineffizient, da Sie auf eine feste Stichprobengröße warten müssen
- Also, sollten Sie sich für Bayesian oder Frequentist entscheiden? Es gibt einen Platz für beide.
- Schlüssel zum Mitnehmen
Bereit? Beginnen wir mit den Grundlagen.
Was ist Bayessche Statistik?
Bayes'sche Statistik ist ein Ansatz zur statistischen Analyse, der auf dem Bayes-Theorem basiert, das Überzeugungen über Ereignisse aktualisiert, wenn neue Daten oder Beweise über diese Ereignisse gesammelt werden. Hier ist die Wahrscheinlichkeit ein Maß für die Überzeugung, dass ein Ereignis eintritt.
Was das bedeutet: Wenn Sie eine frühere Überzeugung über ein Ereignis haben und mehr Informationen darüber erhalten, wird diese Überzeugung in eine spätere Überzeugung geändert (oder zumindest angepasst).
Dies ist nützlich, um Unsicherheiten zu verstehen oder wenn Sie mit vielen verrauschten Daten arbeiten, z. B. bei der Optimierung der Konversionsrate für E-Commerce und beim maschinellen Lernen.
Stellen wir uns das vor:
Nehmen wir zum Beispiel an, Sie sehen sich ein College-Einkaufskarrenrennen an und dann fordert Sie ein aufgeregter Zuschauer zu einer Wette heraus, dass der Typ im roten T-Shirt, der die Dame im grünen Hemd fährt, gewinnt. Du denkst darüber nach und konterst, dass der Typ mit der schwarzen Jacke und das Mädchen mit der schwarzen Kapuze stattdessen gewinnen werden.

Ein anderer Zuschauer über Ihnen flüsterte Ihnen einen Tipp zu: „Der Typ mit dem roten T-Shirt hat die letzten 3 von 4 Rennen gewonnen.“ Was passiert mit Ihrer Wette? Du bist dir nicht mehr sicher, oder?
Angenommen, Sie haben auch erfahren, dass der Typ mit der schwarzen Jacke das letzte Mal, als er seine glückliche Sonnenbrille trug, gewonnen hat. Und die Male, in denen er es nicht trug, gewann der Typ mit dem roten T-Shirt.
Heute sieht man, dass der Typ mit der schwarzen Jacke diese Brille trägt. Ihr Glaube ändert sich erneut. Sie haben jetzt mehr Vertrauen in Ihre Wette, richtig? In dieser Geschichte haben Sie Ihren Glauben jedes Mal aktualisiert, wenn Sie Beweise für neue Daten erhalten haben. Das ist der bayessche Ansatz.
Die Bayes'sche Ursprungsgeschichte
Als Reverend Thomas Bayes zum ersten Mal über seine Theorie nachdachte, hielt er sie für nicht veröffentlichungswürdig. So blieb es über ein Jahrzehnt in seinen Notizen. Als seine Familie Richard Price bat, seine Notizen durchzugehen, entdeckte Price die Notizen, die die Grundlage des Satzes von Bayes bildeten.
Es begann mit einem Gedankenexperiment für Bayes. Er dachte daran, mit dem Rücken zu einem vollkommen flachen und quadratischen Tisch zu sitzen und einen Assistenten einen Ball auf den Tisch werfen zu lassen.
Der Ball konnte überall auf dem Tisch landen, aber Bayes dachte, er könnte erraten, wo er seine Vermutungen mit neuen Informationen aktualisieren würde. Wenn der Ball auf dem Tisch landete, ließ er sich vom Assistenten sagen, ob er links oder rechts, vor oder hinter dem vorherigen Ball gelandet war.
Er bemerkte das und lauschte, als weitere Bälle auf dem Tisch landeten. Mit zusätzlichen Informationen wie dieser stellte er fest, dass er die Genauigkeit seiner Vermutungen mit jedem Wurf verbessern konnte. Dies brachte uns auf die Idee, unser Verständnis zu aktualisieren, da wir mehr Beweise aus der Beobachtung gewonnen haben.
Der Bayes'sche Ansatz zur Datenanalyse wird in verschiedenen Bereichen wie Wissenschaft und Technik angewendet und umfasst sogar Sport und Recht.
In randomisierten kontrollierten Online-Experimenten, insbesondere A/B-Tests, können Sie den Bayes'schen Ansatz in 4 Schritten verwenden:
- Identifizieren Sie Ihre vorherige Distribution.
- Wählen Sie ein statistisches Modell, das Ihre Überzeugungen widerspiegelt.
- Führen Sie das Experiment durch.
- Aktualisieren Sie nach der Beobachtung Ihre Überzeugungen und berechnen Sie eine A-posteriori-Verteilung.
Sie aktualisieren Ihre Überzeugungen mit einem Satz von Regeln, die als Bayes'scher Algorithmus bezeichnet werden.
Ein Beispiel für Bayes'sche Statistik, die auf A/B-Tests angewendet wird
Lassen Sie uns ein Bayes'sches A/B-Testbeispiel veranschaulichen.
Stellen Sie sich vor, wir haben einen einfachen A/B-Test für die CTA-Schaltfläche eines Shopify-Shops durchgeführt. Für „A“ verwenden wir „Add to Cart“ und für „B“ verwenden wir „Add to Your Basket“.
So geht ein Frequentist an den Test heran.
Es gibt zwei alternative Welten: Eine, in der sich A und B nicht unterscheiden, sodass der Test keinen Unterschied in der Conversion-Rate zeigt. Das ist die Nullhypothese. Und in der anderen Welt gibt es einen Unterschied, sodass eine Taste besser funktioniert als die andere.
Der Frequentist wird davon ausgehen, dass wir in Welt 1 leben, wo es keinen Unterschied bei den CTA-Buttons gibt, das heißt, unter der Annahme, dass die Nullhypothese wahr ist. Und dann werden sie versuchen, das Gegenteil mit einem vorher festgelegten Sicherheitsniveau, dem Signifikanzniveau, zu beweisen.
Aber so wird ein Bayesianer an denselben Test herangehen:
Sie beginnen mit der Überzeugung, dass beide Schaltflächen A und B die gleiche Chance haben, eine Conversion-Rate zwischen 0 und 100 % zu erzielen. Es gibt also von Anfang an Gleichberechtigung – beide haben eine 50-prozentige Chance, die Top-Performer zu sein.
Dann beginnt der Test und die Daten werden gesammelt. Durch die Beobachtung neuer Informationen aktualisieren Bayes'sche A/B-Tester ihr Wissen. Wenn B also vielversprechend ist, können sie basierend auf dieser Beobachtung zu einer nachträglichen Überzeugung gelangen, die besagt: „B hat eine Chance von 61 %, A zu schlagen“.
Es gibt grundlegende Unterschiede zwischen den beiden Methoden.
Aus diesem Grund ist es uns wichtig, einen unvoreingenommenen Ansatz für Bayes'sche A/B-Tests beizubehalten.
Die meisten Bayesianischen A/B-Testtools – vielleicht zu Marketingzwecken – nehmen eine extrem anti-frequentistische Haltung ein und argumentieren, dass Bayesianisch besser darin ist, Ihnen zu sagen, welche Variante „profitabler“ ist.
Aber besitzt ein einzelner statistischer Ansatz für A/B-Tests die exklusiven Rechte an Erkenntnissen?
Wenn man das Bayessche Argument weiter vorantreibt, könnten sie mit Studien konfrontiert werden, in denen die Befragten sagen, sie wollen wissen, was die beste Vorgehensweise ist, oder dass sie den Gewinn maximieren wollen oder ähnliches. Damit bewegt sich die Frage fest im entscheidungstheoretischen Bereich – etwas, bei dem weder die bayessche Inferenz noch die frequentistische Inferenz ein direktes Mitspracherecht haben können.
Georgi Georgiev, Schöpfer von Analytics-toolkit.com und Autor von „Statistical Methods in Online A/B Testing“
Wir werden in den folgenden Abschnitten kurz auf diese Details eingehen. Lassen Sie uns zunächst den Rest dieser Einführung leicht verständlich machen.
Ein kurzes Glossar Bayes'scher Begriffe, die für A/B-Tester wichtig sind
Bayessche Inferenz
Bayessche Inferenz aktualisiert die Wahrscheinlichkeit für eine Hypothese mit neuen Daten. Es basiert auf Überzeugungen und Wahrscheinlichkeiten.
Die bayessche Inferenz nutzt die bedingte Wahrscheinlichkeit, um zu verstehen, wie Daten unsere Überzeugungen beeinflussen. Nehmen wir an, wir beginnen mit der Überzeugung, dass der Himmel rot ist. Nachdem wir uns einige Daten angesehen haben, würden wir bald feststellen, dass diese frühere Annahme falsch ist. Wir führen also eine Bayes'sche Aktualisierung durch, um unser falsches Modell über die Farbe des Himmels zu verbessern, und erhalten am Ende eine genauere spätere Annahme .
Michael Berk in Towards Data Science
Bedingte Wahrscheinlichkeit
Die bedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit eines Ereignisses, wenn ein anderes Ereignis eingetreten ist. Das heißt, die Wahrscheinlichkeit von A unter der Bedingung B.
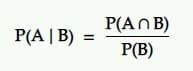
Übersetzung: Die Wahrscheinlichkeit, dass ein Ereignis A eintritt, wenn ein anderes Ereignis B gegeben ist, ist gleich der Wahrscheinlichkeit, dass B und A zusammen eintreten, dividiert durch die Wahrscheinlichkeit von Ereignis B.
Wahrscheinlichkeitsverteilung/Wahrscheinlichkeitsverteilung
Wahrscheinlichkeitsverteilungen sind Verteilungen, die zeigen, wie wahrscheinlich Ihre Daten einen bestimmten Wert annehmen werden.
Wenn Ihre Daten mehrere Werte annehmen können, z. B. eine Kategorie wie Farben, die grau, rot, orange, blau usw. sein können, ist Ihre Verteilung multinomial. Für eine Reihe von Zahlen kann die Verteilung normal sein. Und für Datenwerte, die entweder ja/nein oder wahr/falsch sein könnten, wäre es binomial.
Verteilung der vorherigen Überzeugungen
Oder die Prior-Wahrscheinlichkeitsverteilung, einfach Prior genannt, drückt Ihren Glauben aus, bevor Sie Beweise für neue Daten erhalten haben. Es ist also ein Ausdruck Ihrer anfänglichen Überzeugung, die Sie aktualisieren werden, nachdem Sie einige Beweise unter Verwendung der Bayes'schen Analyse (oder Schlussfolgerung) berücksichtigt haben.
Konjugation
Zuallererst bezieht sich konjugieren darauf, zusammengefügt zu sein, normalerweise paarweise. In der Bayesschen Wahrscheinlichkeitstheorie geht Konjugation davon aus, dass der Prior zur Wahrscheinlichkeit konjugiert ist.
Wenn das Posterior die gleiche funktionale Form wie das Prior hat, dann ist das Prior mit der Likelihood-Funktion konjugiert. Dies zeigt, wie die Wahrscheinlichkeitsfunktion die vorherige Verteilung aktualisiert.
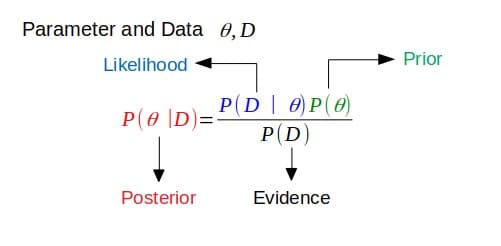
Prioren konjugieren
Dies hängt mit der obigen Definition zusammen. Wenn das Posterior in derselben Wahrscheinlichkeitsverteilungsfamilie ist (oder dieselbe funktionale Form hat) wie die Prior-Wahrscheinlichkeitsverteilung, dann sind das Prior und das Posterior konjugierte Verteilungen. In diesem Fall wird der Prior der konjugierte Prior für die Likelihood-Funktion genannt.
Sie können subjektiv (basierend auf dem Wissen des Experimentators), objektiv und informativ (basierend auf historischen Daten) oder nicht informativ sein.
Verlustfunktion
Eine Verlustfunktion ist eine Möglichkeit, den Verlust zu quantifizieren, indem gemessen wird, wie schlecht unsere aktuelle Schätzung ist. Es hilft uns, den Verlust für Hypothesentests zu minimieren, insbesondere wenn eine Schlussfolgerung ausgedrückt wird, die in einem Bereich wahrscheinlicher Werte liegt, und unterstützt die Entscheidungsfindung mit unseren Testergebnissen.
Jetzt ist das aus dem Weg, wir können weitermachen.
Wenn Sie schon eine Weile um den Block herum sind, sind Sie wahrscheinlich auf mehr als ein paar Statistik-Meme von Frequentisten vs. Bayesianern gestoßen.

Beide Seiten scheinen aus entgegengesetzten Richtungen nach Antworten zu suchen, aber ist das wirklich so? Um dies besser zu verstehen (und dabei unvoreingenommen zu bleiben), besuchen wir das Lager der Frequentisten.
Was ist Frequentistische Statistik?
Dies ist die erste Inferenztechnik, die die meisten Menschen in der Statistik lernen. Frequentistische Statistik berechnet die Wahrscheinlichkeit, dass ein Ereignis (Hypothese) unter gleichen Bedingungen häufig eintritt.
A/B-Hypothesentests mit dem frequentistischen Ansatz folgen diesen Schritten:
- Stellen Sie einige Hypothesen auf. Typischerweise lautet die Nullhypothese, dass die neue Variante „B“ nicht besser ist als die ursprüngliche „A“, während die Alternativhypothese das Gegenteil behauptet.
- Bestimmen Sie im Voraus mithilfe einer statistischen Power-Berechnung eine Stichprobengröße , es sei denn, Sie verwenden sequentielle Testansätze. Verwenden Sie einen Stichprobengrößenrechner, der die statistische Aussagekraft, die aktuelle Konversionsrate und den minimal nachweisbaren Effekt berücksichtigt.
- Führen Sie den Test durch und warten Sie, bis jede Variation der vorher festgelegten Stichprobengröße ausgesetzt ist.
- Berechnen Sie die Wahrscheinlichkeit, ein Ergebnis zu beobachten, das mindestens so extrem ist wie die Daten unter der Nullhypothese (p-Wert). Verwerfen Sie die Nullhypothese und setzen Sie die neue Variante in der Produktion ein, wenn der p-Wert < 5 % ist.
Wie ist das im Vergleich zu Bayesian? Mal schauen…
Bayesianisches vs. Frequentistisches A/B-Testen
Dies ist eine berüchtigte Debatte überall dort, wo statistische Inferenzen verwendet werden. Und um ehrlich zu sein, es ist sinnlos. Beide haben ihre Vorzüge und Fälle, in denen sie die beste Methode sind.
Im Gegensatz zu dem, was die meisten Promoter in beiden Lagern glauben machen werden, sind sie sich in vielerlei Hinsicht ähnlich und keiner kommt der Wahrheit näher als der andere – obwohl ihre Herangehensweisen unterschiedlich sind.
Bei der Anwendung auf A/B-Tests zum Beispiel gibt Ihnen keine spezifische Methode eine absolute und genaue Vorhersage in Bezug auf die Vorgehensweise, die zum Unternehmenswachstum führen wird. Stattdessen helfen Ihnen A/B-Tests, das Risiko aus der Entscheidungsfindung zu entfernen.
Ganz gleich, wie Sie Ihre Daten analysieren – mit Bayes'schen oder Frequentistischen Ansätzen – Sie können mit einem gewissen Maß an Gewissheit handeln, dass Sie richtig liegen.
Und aus diesem Grund sind beide statistischen Modelle gültig. Bayesian hat möglicherweise einen Geschwindigkeitsvorteil, ist jedoch rechenintensiver als Frequentist.
Sehen Sie sich weitere Unterschiede an…
Das Frequentistische Framework
Die meisten von uns kennen den frequentistischen Ansatz aus einführenden Statistikkursen. Wir haben die obige Methodik definiert – von der Deklaration der Nullhypothese, der Bestimmung der Stichprobengröße, der Datenerhebung über ein randomisiertes Experiment bis hin zur Beobachtung eines statistisch signifikanten Ergebnisses.
Im Frequentismus betrachten wir die Wahrscheinlichkeit als grundlegend mit der Häufigkeit wiederholter Ereignisse verbunden. Bei einem fairen Münzwurf glaubt ein Frequentist also, dass er, wenn er häufig genug rät, in 50 % der Fälle Kopf und Zahl richtig trifft.
Frequentistische Denkweise: „Wie stehen die Chancen, dass meine Methode die richtige Antwort liefert, wenn ich das Experiment immer wieder unter den gleichen Bedingungen wiederhole?“
Das Bayessche Framework
Während der frequentistische Ansatz den Populationsparameter für jede Variante als (unbekannte) Konstante behandelt, modelliert der bayessche Ansatz jeden Parameterwert als Zufallsvariable mit einer gewissen Wahrscheinlichkeitsverteilung.
Hier berechnen Sie direkt Wahrscheinlichkeitsverteilungen (und damit Erwartungswerte) für die interessierenden Parameter.
Und um die Wahrscheinlichkeitsverteilung für jede Variante zu modellieren, verlassen wir uns auf die Bayes-Regel, um die Experimentergebnisse mit jeglichem Vorwissen zu kombinieren, das wir über die interessierende Metrik haben. Wir können die Berechnungen vereinfachen, indem wir einen konjugierten Prior verwenden.
Alex Birkett hat den Bayes'schen Algorithmus folgendermaßen zusammengefasst:
- Definieren Sie die vorherige Verteilung, die Ihre subjektiven Überzeugungen zu einem Parameter enthält. Der Prior kann informativ oder informativ sein.
- Daten sammeln.
- Aktualisieren Sie Ihre vorherige Verteilung mit den Daten unter Verwendung des Bayes-Theorems (obwohl Sie Bayessche Methoden ohne explizite Verwendung der Bayes-Regel verwenden können - siehe nichtparametrische Bayessche), um eine spätere Verteilung zu erhalten. Die A-posteriori-Verteilung ist eine Wahrscheinlichkeitsverteilung, die Ihre aktualisierten Überzeugungen über den Parameter darstellt, nachdem Sie die Daten gesehen haben.
- Analysieren Sie die Posterior-Verteilung und fassen Sie sie zusammen (Mittelwert, Median, Standardabweichung, Quantile…).
Kurz gesagt, der Bayesianische Experimentator konzentriert sich auf seine eigene Perspektive und darauf, was Wahrscheinlichkeit für ihn bedeutet. Ihre Meinung entwickelt sich mit beobachteten Daten. Frequentisten hingegen glauben, dass die richtige Antwort irgendwo da draußen liegt.

Verstehen Sie, dass die Debatte zwischen Frequentisten und Bayesianern keinen allzu großen Einfluss auf die Post-A/B-Testanalyse hat. Die Hauptunterschiede zwischen den beiden Lagern beziehen sich eher darauf, was getestet werden kann.
Wahrscheinlichkeitsstatistiken werden in der Regel nicht in großem Umfang in der nachfolgenden Analyse verwendet. Das bayesianisch-frequentistische Argument trifft eher auf die Auswahl der zu testenden Variablen im A/B-Paradigma zu, aber selbst dort verletzen die meisten A/B-Tester höllisch Forschungshypothesen, Wahrscheinlichkeiten und Konfidenzintervalle .
Dr. Rob Balon zu CXL
Georgi führt weiter aus:
Es gibt mehrere Bayessche Online-Rechner und mindestens einen großen Anbieter von A/B-Testsoftware, die eine Bayessche Statistik-Engine verwenden, die alle sogenannte nicht-informative Priors verwenden (eine etwas falsche Bezeichnung, aber lassen Sie uns nicht darauf eingehen). In den meisten Fällen stimmen die Ergebnisse dieser Tools numerisch mit den Ergebnissen eines frequentistischen Tests mit denselben Daten überein. Nehmen wir an, das Bayes'sche Tool meldet so etwas wie „96 % Wahrscheinlichkeit, dass B besser als A ist“, während das frequentistische Tool einen p-Wert von 0,04 erzeugt, was einem Konfidenzniveau von 96 % entspricht.
In einer Situation wie der oben genannten, die weitaus häufiger vorkommt, als manche zugeben möchten, führen beide Methoden zu derselben Schlussfolgerung, und das Maß an Unsicherheit ist gleich, auch wenn die Interpretation unterschiedlich ist.
Was würde ein Bayesianer zu diesem Ergebnis sagen? Wird der p-Wert in eine richtige spätere Wahrscheinlichkeit umgewandelt, wenn ein Szenario betrachtet wird, in dem es keine Vorabinformationen gibt? Oder sind all diese Anwendungen von Bayes'schen Tests fehlgeleitet, um per se einen nicht informativen Prior zu verwenden?
Es ist wirklich nicht nötig, ein Lager auszuwählen und einen Platz hinter der Deckung zu finden, um Steine auf das andere Lager zu werfen. Es gibt sogar Hinweise darauf, dass beide Frameworks die gleichen Ergebnisse liefern. Egal für welche Straße Sie sich entscheiden, das Ziel wird wahrscheinlich dasselbe sein. Es hängt davon ab, wie Sie mit Frequentist vs. Bayesian dorthin gelangen.
Zum Beispiel:
- Es gibt Daten, die zeigen, dass Bayes'sches Testen schneller und die bevorzugte Wahl für interaktive Experimente ist:
Da das Bayes'sche Paradigma es Experimentatoren ermöglicht, den Glauben formal zu quantifizieren und zusätzliches Wissen einzubeziehen, ist es schneller als die traditionelle statistische Analyse.
In einer Bayes'schen A/B-Testsimulation schlossen 75 % der Experimente bei Anpassung des Entscheidungskriteriums (dh Erhöhung der Fehlertoleranz) innerhalb von 22,7 % der Beobachtungen, die für den traditionellen Ansatz erforderlich sind (bei einem Signifikanzniveau von 5 %). Und es wurden nur 10 % Typ-II-Fehler aufgezeichnet. - Bayesian gilt auch als fehlerverzeihender, während Frequentist risikoavers ist:
Während viele Frequentisten-Tests eine statistische Signifikanz von 95 % verwenden, können Bayesianer mit weniger zufrieden sein. Wenn eine Variante eine 78-prozentige Chance hat, die Kontrolle zu schlagen, könnte es abhängig vom erwarteten Verlust eine vernünftige Entscheidung sein, diese Variante einzusetzen.
Wenn Sie sich irren und der erwartete Verlust weniger als ein Prozent beträgt, ist das für viele Unternehmen ein ziemlich unbedeutender Schaden. Dieser bruchstückhafte Ansatz eignet sich möglicherweise besser für eine schnelle Entscheidungsfindung in Szenarien mit sehr geringem Risiko. - Bayes'sche Simulationen und Berechnungen sind jedoch rechenintensiv:
Frequentist hingegen ist stift- und papierbasiert. Achtung: Wenn Ihr A/B-Testtool Bayesian verwendet und Sie nicht wissen, welche Annahmen zu Ihren Daten hinzugefügt werden, können Sie sich nicht auf die „Antwort“ Ihres Anbieters verlassen. Nehmen Sie es mit einer Prise Salz. Und führen Sie Ihre eigene Analyse durch.
Es ist nicht alles Sonnenschein und Regenbögen mit Bayesian. Wie Georgi mit dieser Liste von Fragen betont:
- „Möchten Sie das Produkt aus der A-priori-Wahrscheinlichkeit und der Likelihood-Funktion erhalten?“
- „Möchten Sie die Mischung aus früheren Wahrscheinlichkeiten und Daten als Ausgabe?“
- „Möchten Sie, dass subjektive Überzeugungen mit den Daten gemischt werden, um die Ausgabe zu erzeugen?“ (bei Verwendung informativer Priors)
- „Würden Sie sich damit wohlfühlen, Statistiken zu präsentieren, in denen Vorabinformationen, von denen angenommen wird, dass sie höchst sicher sind, mit den tatsächlichen Daten vermischt sind?“
Dies sind alles Aspekte der Bayes'schen Statistik, in Laiensprache ausgedrückt.
Was sagt Ihnen die Bayes'sche Statistik eigentlich beim A/B-Testen?
Sie haben Ihren A/B-Test so konzipiert, dass er Aufschluss darüber gibt, wie sich eine Änderung auf Ihre interessierende Metrik auswirkt, z. B. die Konversionsrate oder den Umsatz pro Besucher.
Wenn Sie ein Tool verwenden, das mit Bayes'scher Statistik arbeitet, ist es wichtig zu verstehen, was Ihre Ergebnisse bedeuten, denn „B ist der Gewinner“ bedeutet nicht genau das, was die meisten Leute denken.
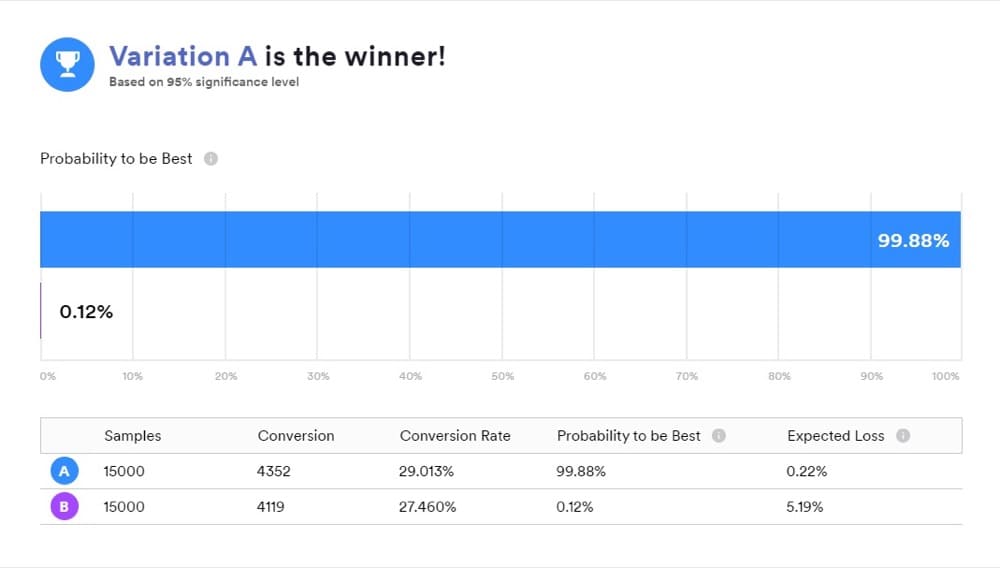
Es ist eine praktische Möglichkeit, Ergebnisse zu präsentieren, aber das hat Ihr Test nicht ergeben. Stattdessen sind die gewünschten Antworten in späteren Vergleichen von „A“ und „B“.
Hier sind die 3 Vergleichsmethoden:
Wahrscheinlichkeit, der Beste zu sein (P2BB)
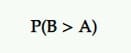
Dies ist die Wahrscheinlichkeit, die einen Sieger in Bayes'schen A/B-Tests erklärt.
Die Variante mit der Wahrscheinlichkeit, die beste zu sein, ist diejenige mit der höchsten Wahrscheinlichkeit, die andere weiterhin zu übertreffen.
Dies wird aus einem Satz späterer Proben des interessierenden Maßes aus dem Original und dem Herausforderer berechnet.
Wenn B also beispielsweise die höchste Wahrscheinlichkeit hat, Ihre Konversionsraten zu steigern, wird B zum Gewinner erklärt.
Erwarteter Aufstieg
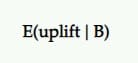
Wenn also B der Gewinner ist, wie viel Auftrieb können wir davon erwarten? Würde es weiterhin die gleichen Ergebnisse liefern, die wir im Test gesehen haben?
Das ist die Einsicht, die der erwartete Auftrieb vermitteln soll. Der erwartete Anstieg bei der Wahl von B gegenüber A bei einer Reihe späterer Stichproben wird als glaubwürdiges Intervall (oder Mittelwert) des prozentualen Anstiegs definiert.
Bei A/B-Tests vergleichen wir dies normalerweise als Herausforderer gegen die Kontrolle. Wenn der Herausforderer also verloren hat, wird dies in negativen Werten (wie -11,35 %) und positiven Werten (wie +9,58 %) dargestellt, wenn er gewonnen hat.
Erwarteter Verlust
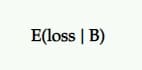
Da es keine 100-prozentige Wahrscheinlichkeit gibt, dass B besser ist als A, besteht die Möglichkeit, dass Sie einen Verlust verbuchen, wenn Sie B statt A wählen. Dies wird als erwarteter Verlust dargestellt und genau wie beim erwarteten Uplift durch den ausgedrückt Sicht des Herausforderers gegen die Kontrolle.
Es zeigt Ihnen das Risiko der Wahl Ihrer P2BB-Variante (dh des erklärten Gewinners).
Bevor wir in die Mythen eintauchen, ein großes Dankeschön an die Analytics-Legende Georgi Georgiev. Seine tiefgehenden Analysen von Frequentisten vs. Bayesianischer Inferenz und Bayesianischer Wahrscheinlichkeit und Statistik in A/B-Tests inspirierten den nächsten Abschnitt.
Mythen rund um die Bayes'sche Statistik, die es zu vermeiden gilt
Mit einer Rivalität, die fast so alt wie unnötig ist, hat die Debatte zwischen Bayesianern und Frequentisten viel Input gesammelt – und viele Mythen entstehen lassen.
Der größte dieser Mythen (Mythos Nr. 2) wird von Anbietern von A/B-Testing-Tools verbreitet, um Ihnen zu erklären, warum ein Ansatz besser ist als der andere.
Aber nachdem Sie die obigen Abschnitte gelesen haben, wissen Sie es besser.
Lassen Sie uns die Lücken in diesen Mythen aufdecken.
Mythos Nr. 1: Bayesianer formulieren ihre Annahmen, Frequentisten nicht
Dies deutet darauf hin, dass Bayesianer Annahmen in Form von vorherigen Verteilungen treffen und diese für eine Bewertung offen sind. Aber Frequentisten machen Annahmen, die in der Mitte der Mathematik verborgen sind.
Warum es falsch ist: Bayesianer und Frequentisten gehen von ähnlichen zugrunde liegenden Annahmen aus, der einzige Unterschied besteht darin, dass Bayesianer zusätzliche Annahmen treffen – zusätzlich zur Mathematik.
Frequentistische Modelle verwenden Annahmen in der Mathematik, wie z. B. die Form der Verteilung, Homogenität oder Heterogenität des Effekts über Beobachtungen hinweg und die Unabhängigkeit der Beobachtung. Und sie sind nicht versteckt. Tatsächlich werden sie in der Statistik-Community breit diskutiert und für jeden frequentistischen statistischen Test angegeben.
Die Wahrheit: Frequentisten formulieren ihre Annahmen explizit und gehen noch einen Schritt weiter, um die Annahmen zu testen: Tests auf Normalität, Test auf Anpassungsgüte (unter denen wir den Stichprobenverhältnis-Mismatch-Test haben) und mehr.
Mythos Nr. 2. Bayesianische Methoden geben Ihnen die Antworten, die Sie wirklich wollen
Das Missverständnis hier ist, dass p-Werte und Konfidenzintervalle den Testern nicht sagen, was sie wissen wollen, während spätere Wahrscheinlichkeiten und glaubwürdige Intervalle dies tun. Die Leute wollen Dinge wissen wie
- Die Wahrscheinlichkeit, dass B A übertrifft und
- Die Wahrscheinlichkeit, dass das Ergebnis kein Zufall ist.
P-Werte und Hypothesentests (gerade Inferenz) liefern diese Informationen nicht, aber inverse Inferenz.
Warum es falsch ist: Das ist eine Frage der Linguistik. Wenn Nicht-Statistiker Begriffe wie „Wahrscheinlichkeit“, „Zufall“ und „Wahrscheinlichkeit“ verwenden, verwenden sie im Allgemeinen nicht ihre technische Bedeutung. Wenn Sie genauer nachforschen, werden Sie feststellen, dass sie über umgekehrte Schlussfolgerungen genauso verwirrt sind wie über direkte Schlussfolgerungen.
Laut Georgi Georgiev tauchen Fragen wie diese auf:
- „ Was ist eine vorherige Wahrscheinlichkeit? Welchen Wert bringt es?“
- „Was ist eine Wahrscheinlichkeitsfunktion?“
- "Welche 'Vorher'-Wahrscheinlichkeit, ich habe keine Vordaten?"
- „Wie verteidige ich die Wahl einer A-priori-Wahrscheinlichkeit?“
- „Gibt es eine Möglichkeit, genau das zu kommunizieren, was die Daten aussagen, ohne diese Mischungen?“
Die Wahrheit: Es sollte einen besseren Einblick in das geben, was Tester wissen wollen, und nicht in ihre Fehlinterpretation von Fachbegriffen. P-Werte, Konfidenzintervalle und andere sagen Ihnen, wie gut die Ergebnisse mit den gesammelten Daten untersucht werden. Sie boten ein Maß an Sicherheit ohne den Einfluss subjektiver, nicht getesteter vorheriger Annahmen.
Mythos Nr. 3: Bayes'sche Inferenz hilft Ihnen, Unsicherheit besser zu kommunizieren als häufige Inferenz
Weil die Ergebnisse der Tests „aussagekräftigere“ Erkenntnisse liefern.
Warum es falsch ist: Sowohl der Frequentistische als auch der Bayesianische Ansatz verfügen über ähnliche Tools, mit denen Sie Gewissheit und die Ergebnisse Ihres A/B-Tests kommunizieren können.
| Frequentist | Bayesianisch | ||||||||||
| ● Punktschätzungen | ● Punktschätzungen | ||||||||||
| ● P-Werte | ● Glaubwürdige Intervalle | ||||||||||
| ● Konfidenzintervalle | ● Bayes-Faktoren | ||||||||||
| ● P-Wert-Kurven | ● Spätere Verteilungen (erledige die gleiche Aufgabe wie die Frequentistenkurven) | ||||||||||
| ● Vertrauenskurven | |||||||||||
| ● Schweregradkurven usw. |
Die Wahrheit: Es hängt alles davon ab, wie Sie sie verwenden. Beide Methoden sind gleichermaßen wirksam bei der Kommunikation von Unsicherheit. Es gibt jedoch Unterschiede in der Darstellung des Unsicherheitsmaßes.
Mythos Nr. 4. Bayes'sche A/B-Testergebnisse sind immun gegen Peeking
Einige Bayes'sche Statistiker argumentieren, dass man einen Bayes'schen Test beenden kann, sobald man einen „klaren Sieger“ sieht und es am Endergebnis kaum einen Unterschied macht.
Sie wissen wahrscheinlich, dass dies in Frequentist-Tests nicht akzeptabel ist, daher wird es im Vergleich zu Bayesian als Nachteil gewertet. Aber ist es das wirklich?
Warum es falsch ist: In einer Studie aus dem Jahr 1969 im Journal of the Royal Statistical Society mit dem Titel „Repeated Significance Tests on Accumulating Data“ stellten Armitage et al. zeigten, wie ergebnisbasiertes optionales Stoppen die Fehlerwahrscheinlichkeit erhöht.
Sie können nicht einfach aufhören, wenn Sie einen Gewinner bemerken, Ihren Posterior aktualisieren und ihn als nächsten Prior verwenden, ohne die Funktionsweise der Bayes'schen Analyse anzupassen.
Die Wahrheit: Peeking beeinflusst die Bayessche Inferenz genauso wie Frequentist (wenn Sie es richtig machen wollen).
Mythos Nr. 5. Frequentistische Statistiken sind ineffizient, da Sie auf eine feste Stichprobengröße warten müssen
Einige Mitglieder der CRO-Community glauben, dass frequentistische statistische Tests mit einer festen, vorher festgelegten Stichprobengröße durchgeführt werden müssen, da sonst die Ergebnisse ungültig sind.
Infolgedessen warten Sie länger als nötig, um die gewünschten Ergebnisse zu erzielen.
Warum es falsch ist: Frequentistische Statistiken werden seit etwa sieben Jahrzehnten nicht mehr auf diese Weise verwendet. Bei frequentistischen sequentiellen Tests benötigen Sie keine fest vorgegebene Dauer.
Die Wahrheit: Sequenzielle Tests, die heute beliebter sind, erfordern eine maximale Stichprobengröße, um Typ-I- und Typ-II-Fehler auszugleichen, aber die tatsächlich verwendete Stichprobengröße variiert von Fall zu Fall je nach beobachtetem Ergebnis.
Also, sollten Sie sich für Bayesian oder Frequentist entscheiden? Es gibt einen Platz für beide.
Es ist nicht nötig, sich für eine Seite zu entscheiden. Beide Methoden haben ihre Berechtigung. Zum Beispiel ist ein langfristiges Projekt, das aktualisierte Priors verwendet und schnelle Ergebnisse benötigt, besser mit dem Bayes'schen Ansatz kompatibel.
Die Frequentistische Methode hingegen eignet sich am besten für Projekte, die ein hohes Maß an Wiederholbarkeit ihrer Ergebnisse erfordern. Zum Beispiel beim Schreiben von Software, die viele Menschen mit vielen Datensätzen verwenden werden.
Wie Cassie Kozyrkov, Head of Decision Intelligence bei Google, sagt: „Statistik ist die Wissenschaft der Meinungsänderung unter Unsicherheit“.
In ihrem zusammenfassenden Video Bayesian vs Frequentist Statistics sagte sie:
„Sie können diese Frequentisten- und Bayesianische Debatte nehmen und alles auf das reduzieren, worüber Sie Ihre Meinung ändern. Frequentisten ändern ihre Meinung über Aktionen, sie haben eine bevorzugte Standardaktion – vielleicht haben sie keine Überzeugungen – aber sie haben eine Aktion, die sie unter Unwissenheit mögen, und dann fragen sie: „Ändern meine Beweise [oder Daten] meine Meinung darüber diese Aktion?“ „Fühle ich mich aufgrund meiner Beweise lächerlich, wenn ich das mache?“
Bayesianer hingegen ändern ihre Meinung auf andere Weise. Sie beginnen mit einer Meinung, einer mathematisch ausgedrückten persönlichen Meinung, die Prior genannt wird, und dann fragen sie: „Was ist die vernünftige Meinung, die ich haben sollte, nachdem ich einige Beweise aufgenommen habe?“ Und so ändern Frequentisten ihre Meinung über Handlungen, Bayesianer ändern ihre Meinung über Überzeugungen.
Und je nachdem, wie Sie Ihre Entscheidungsfindung gestalten möchten, ziehen Sie es vielleicht vor, sich für ein Lager gegenüber dem anderen zu entscheiden.“
Am Ende gehen wir alle auf ähnliche Schlussfolgerungen zu – der Unterschied besteht darin, wie diese Schlussfolgerungen Ihnen präsentiert werden.
Wenn frequentistische und bayessche Inferenz Programmierfunktionen wären und Eingaben statistische Probleme wären, dann würden sich die beiden darin unterscheiden, was sie an den Benutzer zurückgeben. Die frequentistische Inferenzfunktion würde eine Zahl zurückgeben, die eine Schätzung darstellt (normalerweise eine zusammenfassende Statistik wie der Stichprobendurchschnitt usw.), während die Bayes'sche Funktion Wahrscheinlichkeiten zurückgeben würde.
Auszug aus dem Buch „Probabilistic Programming & Bayesian Methods for Hackers
Was nicht ganz richtig ist, ist die Behauptung, dass das eine mehr praktische Ergebnisse liefert als das andere.
Schlüssel zum Mitnehmen
Bayes'sche Statistik im A/B-Testing besteht aus 4 verschiedenen Schritten:
- Identifizieren Sie Ihre vorherige Distribution
- Wählen Sie ein statistisches Modell, das Ihre Überzeugungen widerspiegelt
- Führen Sie das Experiment durch
- Verwenden Sie die Ergebnisse, um Ihre Überzeugungen zu aktualisieren und eine A-posteriori-Verteilung zu berechnen
Ihre Ergebnisse weisen Sie auf aufschlussreiche Wahrscheinlichkeiten hin. So wissen Sie, welche Variante die höchste Wahrscheinlichkeit hat, die beste zu sein, Ihren erwarteten Verlust und Ihren erwarteten Anstieg.
Diese werden in der Regel von den meisten A/B-Testing-Tools mithilfe von Bayes-Statistiken für Sie interpretiert. Ein gründlicher Experimentator wird jedoch eine Post-Test-Analyse durchführen, um diese Ergebnisse besser zu verstehen.
Weil Sie es bis hierher geschafft haben, hier ein Fun Fact für Sie: Kennen Sie das Porträt von Thomas Bayes, das jeder kennt? Dieses:

Niemand ist sich hundertprozentig sicher, dass er es ist.