أخطاء النوع الأول والنوع الثاني: الأخطاء الحتمية في التحسين

تحدث أخطاء النوع الأول والنوع الثاني عندما تكتشف عن طريق الخطأ الفائزين في تجاربك أو تفشل في تحديدهم. مع كلا الخطأين ، ينتهي بك الأمر مع ما يبدو أنه يعمل أم لا. وليس بالنتائج الحقيقية.

لا يؤدي سوء تفسير نتائج الاختبار إلى جهود تحسين مضللة فحسب ، بل قد يؤدي أيضًا إلى تعطيل برنامج التحسين الخاص بك على المدى الطويل.

أفضل وقت للقبض على هذه الأخطاء هو قبل أن تقوم بها! لذلك دعونا نرى كيف يمكنك تجنب الوقوع في أخطاء النوع الأول والنوع الثاني في تجارب التحسين الخاصة بك.

لكن قبل ذلك ، دعونا نلقي نظرة على الفرضية الصفرية ... لأنها الرفض الخاطئ أو عدم الرفض للفرضية الصفرية هو الذي يسبب أخطاء من النوع الأول والنوع الثاني .

الفرضية الفارغة: H0

عندما تفترض تجربة ما ، لا تقفز مباشرةً للاقتراح بأن التغيير المقترح سينقل مقياسًا معينًا.

تبدأ بالقول إن التغيير المقترح لن يؤثر على المقياس المعني على الإطلاق - وأنهم غير مرتبطين.

هذه هي فرضيتك الصفرية (H0). H0 هو دائما أنه لا يوجد تغيير. هذا ما تعتقده ، بشكل افتراضي ... حتى (وإذا) تدحضه تجربتك.

وفرضيتك البديلة (Ha أو H1) هي أن هناك تغييرًا إيجابيًا. H0 و Ha هما دائمًا متضادان رياضيان. Ha هو الشخص الذي تتوقع أن يحدث التغيير المقترح فيه فرقًا ، إنها فرضيتك البديلة - وهذا ما تختبره بتجربتك.

لذلك ، على سبيل المثال ، إذا كنت ترغب في إجراء تجربة على صفحة التسعير الخاصة بك وإضافة طريقة دفع أخرى إليها ، فعليك أولاً تكوين فرضية فارغة تقول: لن يكون لطريقة الدفع الإضافية أي تأثير على المبيعات. ستقرأ الفرضية البديلة: طريقة الدفع الإضافية ستزيد المبيعات.

إجراء تجربة ، في الواقع ، يتحدى الفرضية الصفرية أو الوضع الراهن.

تحدث أخطاء النوع الأول والنوع الثاني عندما ترفض أو تفشل في رفض الفرضية الصفرية.

فهم أخطاء النوع الأول

تُعرف أخطاء النوع الأول بالإيجابيات الزائفة أو أخطاء ألفا.

في مثيل خطأ من النوع الأول لاختبار الفرضية ، يبدو أن اختبار التحسين أو تجربتك * يبدو ناجحًا * وتستنتج (خطأ) أن الشكل الذي تختبره يعمل بشكل مختلف (أفضل أو أسوأ) عن الأصل.

في أخطاء النوع الأول ، ترى ارتفاعات أو انخفاضات - وهي مؤقتة فقط ومن المحتمل ألا تستمر على المدى الطويل - وينتهي بك الأمر برفض فرضيتك الصفرية (وقبول فرضيتك البديلة).

يمكن أن يحدث الرفض الخاطئ للفرضية الصفرية لأسباب مختلفة ، ولكن السبب الرئيسي هو ممارسة النظرة الخاطفة (أي النظر إلى نتائجك في غضون ذلك أو عندما تكون التجربة لا تزال قيد التنفيذ). واستدعاء الاختبارات في وقت أقرب من الوصول إلى معايير التوقف المحددة.

لا تشجع العديد من منهجيات الاختبار ممارسة النظرة الخاطفة لأن النظر في النتائج المؤقتة قد يؤدي إلى استنتاجات خاطئة تؤدي إلى أخطاء من النوع الأول.

إليك كيفية ارتكاب خطأ من النوع الأول:

لنفترض أنك تقوم بتحسين الصفحة المقصودة لموقع الويب B2B الخاص بك وافترض أن إضافة شارات أو جوائز إليها ستقلل من قلق العملاء المحتملين ، وبالتالي زيادة معدل تعبئة النموذج الخاص بك (مما يؤدي إلى المزيد من العملاء المتوقعين).

لذا تصبح فرضيتك الصفرية لهذه التجربة: إضافة الشارات ليس لها تأثير على تعبئة النموذج.

عادة ما تكون معايير التوقف لمثل هذه التجربة فترة معينة و / أو بعد حدوث تحويلات X على مستوى الأهمية الإحصائية المحدد. بشكل تقليدي ، يحاول المحسِّنون الوصول إلى علامة الثقة الإحصائية 95٪ لأنها تترك لك فرصة بنسبة 5٪ لارتكاب الخطأ من النوع الأول الذي يعتبر منخفضًا بدرجة كافية لمعظم تجارب التحسين. بشكل عام ، كلما ارتفع هذا المقياس ، قلت فرص ارتكاب أخطاء من النوع الأول.

يحدد مستوى الثقة الذي تهدف إليه ما هو احتمال حصولك على خطأ من النوع الأول (α).

لذلك إذا كنت تهدف إلى مستوى ثقة بنسبة 95٪ ، فإن القيمة الخاصة بك لـ α تصبح 5٪. هنا ، أنت تقبل أن هناك احتمال بنسبة 5٪ أن يكون استنتاجك خاطئًا.

في المقابل ، إذا ذهبت بمستوى ثقة بنسبة 99٪ في تجربتك ، فإن احتمالية حصولك على خطأ من النوع الأول تنخفض إلى 1٪.

لنفترض ، بالنسبة لهذه التجربة ، أنك أصبحت غير صبور للغاية وبدلاً من انتظار انتهاء تجربتك ، نظرت إلى لوحة معلومات أداة الاختبار الخاصة بك (نظرة خاطفة!) بعد يوم واحد منها. ولاحظت ارتفاعًا "واضحًا" - حيث ارتفع معدل تعبئة النموذج بنسبة هائلة بلغت 29.2٪ مع مستوى ثقة بنسبة 95٪.

و بام ...

... توقف تجربتك.

... رفض فرضية العدم (أن الشارات لم يكن لها أي تأثير على المبيعات).

… قبول الفرضية البديلة (أن الشارات عززت المبيعات).

... وتشغيل الإصدار مع شارات الجوائز.

ولكن عندما تقيس العملاء المتوقعين على مدار الشهر ، تجد أن الرقم يمكن مقارنته تقريبًا بما أبلغت عنه في الإصدار الأصلي. لم تكن الشارات مهمة كثيرًا بعد كل شيء. وأن فرضية العدم ربما تم رفضها عبثًا.

ما حدث هنا هو أنك أنهيت تجربتك في وقت مبكر جدًا ورفضت الفرضية الصفرية وانتهى بك الأمر بفائز خاطئ - ارتكاب خطأ من النوع الأول.

تجنب أخطاء النوع الأول في تجاربك

تتمثل إحدى الطرق المؤكدة لتقليل فرصك في الوصول إلى خطأ من النوع الأول بمستوى ثقة أعلى. يعتبر مستوى الدلالة الإحصائية بنسبة 5٪ (الترجمة إلى مستوى ثقة إحصائي بنسبة 95٪) مقبولاً. إنه رهان سيجعله معظم المحسّنين بأمان لأنك ستفشل هنا في نطاق 5٪ غير محتمل.

بالإضافة إلى تعيين مستوى ثقة عالي ، فإن إجراء الاختبارات لفترة كافية أمر مهم. يمكن لآلات حاسبة مدة الاختبار أن تخبرك بالمدة التي يجب أن تجري فيها اختبارك (بعد أخذ أشياء مثل حجم التأثير المحدد من بين أشياء أخرى). إذا سمحت لإحدى التجارب بتنفيذ مسارها المقصود ، فإنك تقلل بشكل كبير فرصك في مواجهة الخطأ من النوع 1 (نظرًا لأنك تستخدم مستوى ثقة مرتفعًا). يضمن الانتظار حتى تصل إلى نتائج ذات دلالة إحصائية أن هناك فرصة ضئيلة (5٪ عادةً) لرفض الفرضية الصفرية عن طريق الخطأ وارتكبت خطأ من النوع الأول. بمعنى آخر ، استخدم حجم عينة جيد لأن ذلك ضروري للحصول على نتائج ذات دلالة إحصائية.

الآن كان هذا كل شيء عن أخطاء النوع الأول المتعلقة بمستوى الثقة (أو الأهمية) في تجاربك. ولكن هناك نوعًا آخر من الأخطاء أيضًا يمكن أن يتسلل إلى اختباراتك - أخطاء النوع الثاني.

فهم أخطاء النوع الثاني

تُعرف أخطاء النوع الثاني باسم السلبيات الزائفة أو أخطاء بيتا.

على النقيض من الخطأ من النوع الأول ، في حالة حدوث خطأ من النوع الثاني ، تبدو التجربة * غير ناجحة (أو غير مقنعة) * وأنت (خطأ) تستنتج أن الشكل الذي تختبره لا يختلف عن أصلي.

في أخطاء النوع الثاني ، تفشل في رؤية المصاعد أو الانخفاضات الحقيقية وينتهي بك الأمر بالفشل في رفض الفرضية الصفرية ورفض الفرضية البديلة.

إليك كيفية ارتكاب الخطأ من النوع الثاني:

العودة إلى نفس موقع الويب B2B من أعلى ...

لذا افترض هذه المرة أنك تفترض أن إضافة إخلاء مسؤولية الامتثال للائحة العامة لحماية البيانات بشكل بارز في الجزء العلوي من النموذج الخاص بك سيشجع المزيد من العملاء المحتملين على ملئه (مما يؤدي إلى المزيد من العملاء المتوقعين).

لذلك ، تصبح فرضيتك الصفرية لهذه التجربة: إخلاء مسؤولية الامتثال للقانون العام لحماية البيانات (GDPR) لا يؤثر على تعبئة النماذج.

تقرأ الفرضية البديلة لنفس الشيء: ينتج عن إخلاء المسؤولية عن الامتثال للقانون العام لحماية البيانات (GDPR) المزيد من تعبئة النماذج.

تحدد القوة الإحصائية للاختبار مدى قدرته على اكتشاف الاختلافات في أداء نسختك الأصلية والمنافسة ، في حالة وجود أي انحرافات. تقليديا ، يحاول المحسنون الوصول إلى علامة القوة الإحصائية 80 ٪ لأنه كلما ارتفع هذا المقياس ، قلت فرص ارتكاب أخطاء من النوع الثاني.

تأخذ القوة الإحصائية قيمة بين 0 و 1 (وغالبًا ما يتم التعبير عنها في٪) وتتحكم في احتمال الخطأ من النوع الثاني (β) ؛ يتم حسابها على النحو التالي: 1 -

كلما زادت القوة الإحصائية لاختبارك ، انخفض احتمال مواجهة أخطاء من النوع الثاني.

لذلك إذا كانت التجربة ذات قوة إحصائية 10٪ ، فيمكن أن تكون معرضة تمامًا لخطأ من النوع الثاني. في حين أنه إذا كانت التجربة تتمتع بقوة إحصائية تبلغ 80٪ ، فسيكون احتمال ارتكابها لخطأ من النوع الثاني أقل احتمالاً بكثير.

مرة أخرى ، تقوم بإجراء اختبارك ، لكن هذه المرة لا تلاحظ أي زيادة ملحوظة في تعبئة النموذج الخاص بك. كلا الإصدارين يبلغان عن قرب تحويلات مماثلة. وبسبب ذلك ، توقف تجربتك وتستمر في الإصدار الأصلي بدون إخلاء المسؤولية من الامتثال للائحة العامة لحماية البيانات (GDPR).

ومع ذلك ، عندما تتعمق في بيانات العملاء المحتملين من فترة التجربة ، تجد أنه في حين أن عدد العملاء المتوقعين من كلا الإصدارين (النسخة الأصلية والمتحدي) بدا متطابقًا ، فإن إصدار القانون العام لحماية البيانات قد جعلك تحصل على زيادة جيدة وكبيرة في العدد من العملاء المحتملين من أوروبا. (بالطبع ، كان بإمكانك استخدام استهداف الجمهور لإظهار التجربة فقط للعملاء المحتملين من أوروبا - ولكن هذه قصة أخرى.)

ما حدث هنا هو أنك أنهيت الاختبار في وقت مبكر جدًا ، دون التحقق مما إذا كنت قد حصلت على قوة كافية - ارتكاب خطأ من النوع الثاني.

تجنب أخطاء النوع الثاني في تجاربك

لتجنب أخطاء النوع الثاني ، قم بإجراء اختبارات بقوة إحصائية عالية. حاول تكوين تجاربك حتى تتمكن من الوصول إلى 80٪ على الأقل من علامة القوة الإحصائية. هذا مستوى مقبول من القوة الإحصائية لمعظم تجارب التحسين. باستخدامه ، يمكنك التأكد من أنه في 80٪ من الحالات ، على الأقل ، سترفض فرضية فارغة خاطئة بشكل صحيح.

للقيام بذلك ، تحتاج إلى إلقاء نظرة على العوامل التي تضيف إليه.

أكبرها هو حجم العينة (بالنظر إلى حجم التأثير الملحوظ). حجم العينة يرتبط مباشرة بقوة الاختبار. حجم العينة الضخم يعني اختبار قدرة عالية. الاختبارات ضعيفة القوة معرضة بشدة لأخطاء النوع الثاني حيث تقل فرصك في اكتشاف الاختلافات في نتائج منافسيك والإصدارات الأصلية بشكل كبير ، خاصة بالنسبة إلى MEI منخفضة (المزيد حول هذا أدناه). لذلك لتجنب أخطاء النوع الثاني ، انتظر حتى يجمع الاختبار طاقة كافية لتقليل أخطاء النوع الثاني. من الناحية المثالية ، في معظم الحالات ، قد ترغب في الوصول إلى قوة لا تقل عن 80٪.

عامل آخر هو الحد الأدنى من تأثير الاهتمام (MEI) الذي تستهدفه لتجربتك. MEI (يُطلق عليه أيضًا MDE) هو الحد الأدنى لحجم الاختلاف الذي تريد اكتشافه في KPI المعني. إذا قمت بتعيين MEI منخفض (تتطلع إلى زيادة بنسبة 1.5٪ ، على سبيل المثال) ، فإن فرصك في مواجهة الخطأ من النوع الثاني تزداد لأن اكتشاف الاختلافات الصغيرة يحتاج إلى أحجام عينات أكبر بشكل كبير (للحصول على طاقة كافية).

وأخيرًا ، من المهم ملاحظة أنه تميل إلى أن تكون هناك علاقة عكسية بين احتمال ارتكاب خطأ من النوع الأول (α) واحتمال ارتكاب خطأ من النوع الثاني (β). على سبيل المثال ، إذا قمت بتقليل قيمة α لتقليل احتمال ارتكاب خطأ من النوع الأول (لنفترض أنك قمت بتعيين α عند 1٪ ، مما يعني مستوى ثقة بنسبة 99٪) ، فإن القوة الإحصائية لتجربتك (أو قدرتها ، ، من اكتشاف الاختلاف عند وجوده) يؤدي إلى تقليله أيضًا ، وبالتالي زيادة احتمالية حصولك على خطأ من النوع الثاني.

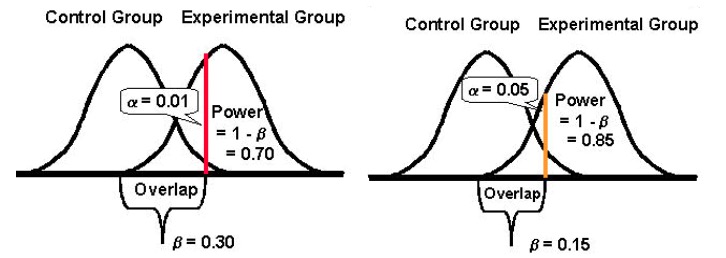
زيادة قبول أي من الخطأين: النوع الأول والثاني (وتحقيق التوازن)

يؤدي خفض احتمالية حدوث نوع واحد من الخطأ إلى زيادة احتمال حدوث نوع آخر (نظرًا لأن كل شيء آخر يظل كما هو).

ولذا فأنت بحاجة إلى الرد على نوع الخطأ الذي يمكن أن تكون أكثر تسامحًا تجاهه.

إن ارتكاب خطأ من النوع الأول ، من ناحية ، وإدخال تغيير لجميع المستخدمين قد يكلفك التحويلات والأرباح - والأسوأ من ذلك ، قد يكون قاتلًا للتحويل أيضًا.

من ناحية أخرى ، فإن ارتكاب خطأ من النوع الثاني ، والفشل في طرح إصدار فائز لجميع المستخدمين لديك ، يمكن أن يكلفك مرة أخرى التحويلات التي كان من الممكن أن تكسبها بخلاف ذلك.

بشكل ثابت ، كلا الخطأين يأتيان بتكلفة.

ومع ذلك ، بناءً على تجربتك ، قد تكون إحداها أكثر قبولًا لك على الأخرى. بشكل عام ، يجد المختبرون خطأ النوع الأول أكثر خطورة بأربع مرات من الخطأ من النوع الثاني .

إذا كنت ترغب في اتباع نهج أكثر توازناً ، فإن الإحصائي جاكوب كوهين يقترح عليك البحث عن قوة إحصائية بنسبة 80٪ تأتي مع " توازن معقول بين مخاطر ألفا وبيتا. "(80٪ من الطاقة هي أيضًا المعيار لمعظم أدوات الاختبار.)

وبقدر ما يتعلق الأمر بالدلالة الإحصائية ، تم تعيين المعيار عند 95٪.

في الأساس ، يتعلق الأمر بالحل الوسط ومستوى المخاطر الذي ترغب في تحمله. إذا كنت تريد حقًا تقليل فرص حدوث كلا الخطأين ، فيمكنك الحصول على مستوى ثقة بنسبة 99٪ وقوة 99٪. لكن هذا يعني أنك ستعمل بأحجام عينات ضخمة بشكل مستحيل لفترات تبدو طويلة إلى الأبد. علاوة على ذلك ، حتى في هذه الحالة سوف تترك مجالًا للأخطاء.

بين الحين والآخر ، ستنهي التجربة بشكل خاطئ. لكن هذا جزء من عملية الاختبار - يستغرق الأمر بعض الوقت لإتقان إحصائيات اختبار A / B. يعد التحقيق وإعادة الاختبار أو متابعة تجاربك الناجحة أو الفاشلة إحدى الطرق لإعادة تأكيد نتائجك أو اكتشاف أنك ارتكبت خطأً.