اشعر بحساب التفاضل والتكامل مع حاسة البرمجة لديك

أعتقد أن الأشخاص الذين يمكنهم البرمجة - لديهم القدرة على فهم مفاهيم أكثر تعقيدًا من حساب التفاضل والتكامل. أحد أسباب وجود العديد من المبرمجين الموهوبين الذين ما زالوا يعانون من التفاضل والتكامل ليس صعوبة ذلك. يرجع ذلك في الغالب إلى أننا تعلمناها بطريقة خاطئة (جنبًا إلى جنب مع العديد من الموضوعات الأخرى).

إذا كنت قد قمت ببعض الترميز في حياتك - حتى بعض تمارين الألعاب مثل توليد الأعداد الأولية ، فربما تكون قد قمت بالفعل بأشياء مماثلة تحدث في حساب التفاضل والتكامل ولكن لم تتح لك الفرصة أبدًا للتواصل.

الهدف من هذه الكتابة ليس تعليمك التفاضل والتكامل أو البرمجة - ولكن لمساعدتك على ربط بعض النقاط.

سأصل إلى جزء الترميز خلال دقيقة. لكن اسمحوا لي أن أقدم بعض المعلومات الأساسية قبل ذلك.

معدل التغيير

يتحدث حساب التفاضل عن "معدل التغيير". دعنا نحاول فهم ما يعنيه ذلك.

بالنسبة للتغيير في المتغير (س) ، فإن معدل تغير الوظيفة هو ببساطة التغيير في الدالة مقسومًا على التغيير في x. دعنا نتخيل بالأرقام الفعلية:

ضع في اعتبارك نقطتين x = 2 و x = 6 والدالة y = f (x) = x².

ضع في اعتبارك أيضًا أن dx = المسافة بين هاتين النقطتين في المحور x. و dy هي المسافة بين قيم y لقيم x هذه.

إذن ، معدل التغير في y من x = 2 إلى x = 6 هو

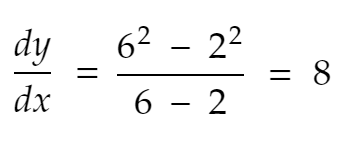
المشتق

الآن - المشتق dy / dx هو معدل التغير في y لتغير ضئيل للغاية في x. نظرًا لأن هذه المسافة (6-2 = 4) ليست صغيرة جدًا - ولا حتى قريبة ، لا يمكننا تسمية المعادلة أعلاه بالمشتق. لذلك ، دعنا نختار رقمًا أصغر ، وهو 0.1 ، في الوقت الحالي.

عندما x = 0 ، y = x² = 0² = 0.

أقرب جار للاتجاه الموجب ، x = 0.1. يصبح y 0.1² = 0.01.

لذا،

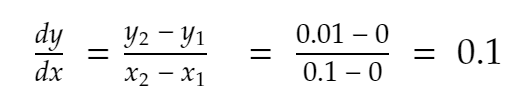
لنجرب مرة أخرى. أقرب جار من 0.1 للاتجاه الموجب ، x = 0.2. إذن ، y تصبح 0.2² = 0.04. لذا،

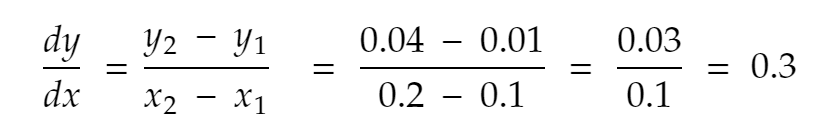
إذا كررنا العملية عدة مرات ، فهذا ما نحصل عليه:

هذا هو ملف Excel إذا كنت ترغب في اللعب به.

dx (وهي مسافة خيالية متناهية الصغر بين نقطتين متجاورتين على المحور x) تساوي 0.1 في سياقنا.

x يتزايد وفقًا لذلك.

y هي ببساطة x².

dy هي المسافة بين قيمتي y المتجاورتين. على سبيل المثال ، عندما تكون x = 0.1 ، تكون المسافة بين y الحالي (0.01) و y التالي (0.04) هي 0.03 - لذا ، dy تساوي 0.03 عند x = 0.1.

dy / dx يساوي dy على dx.

dy / dx / x هو dy / dx مقسومًا على x.

لاحظ الآن أنه مع زيادة x ، فإن الصف الأخير يقترب من 2 ، مما يعني أن معدل تغير x² بالنسبة إلى x يقترب من ضعف x ، وهو 2x .

تذكر مشتق x² بالنسبة إلى x؟ 2x! هل تجد بعض الاتصال؟

وقت الترميز

لنجرب الأشياء الموجودة في الكود التي كنا نناقشها حتى الآن.

بافتراض أنك قمت بالفعل بتثبيت Python ، في المحطة ، قم بتشغيل:

بعد ذلك ، قم بتشغيل كود Python التالي:

هنا:

x : تحتوي على أرقام من 0 إلى 9.

y : مصفوفة أخرى ، كل عنصر هو مربع من عنصر x المقابل

dy : مصفوفة أخرى تمت تهيئتها باستخدام الأصفار. سنضع مسافات y في هذه المصفوفة.

dydx : مصفوفة أخرى تمت تهيئتها باستخدام الأصفار. سيحتوي على قيمة dy / dx لكل نقطة.

dx : واضح جدًا - هو حجم الخطوة. المسافة بين رقمين متتاليين ، والتي تقل بزيادة الحجم. إذا كان الحجم = 10 ، dx = 1. إذا كان الحجم = 100 ، dx = 0.1.

أولاً ، نحن نشتق dy لكل نقطة. ثم نحسب dydx منه.

لاحظ أن:

نحن هنا نحذف القيم الأولى والأخيرة. أول قيمة لـ x هي 0 ، والتي ستنتج خطأ قسمة صفرية. ولا يمكننا حساب القيمة الأخيرة لـ dy / dx نظرًا لأنه ليس لدينا آخر قيمة لـ dy - لأنها تتطلب بجوار آخر قيمة متاحة لـ y ، وهو ما ليس لدينا هنا.

إذا سارت الأمور على ما يرام ، فستحصل على هذا الرسم البياني:

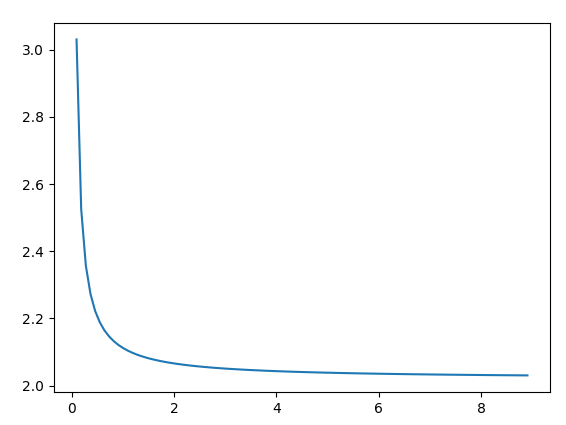
ما تفهمه من المؤامرة

كما ترى ، يقترب الرسم البياني من 2. قم بزيادة قيمة SIZE (مما يعني تعيين قيمة أقل من dx) وشاهد كيف يقترب الرسم البياني بسرعة أكبر 2.

المشتق الثاني

الآن بعد أن وصلت إلى هذا الحد ، ما عليك سوى بضع خطوات أخرى لإدراك المشتق الثاني ، والذي سيمنحك الحدس لمشتقة أي ترتيب.

كما تتذكر ، فإن المشتق الثاني هو معدل تغير المشتق الأول بالنسبة إلى x. ببساطة - dy / dx في المشتق الثاني يشبه y في المشتق الأول.

لنقم بالتعديلات التالية على الكود أعلاه:

قم بتعريف مصفوفتين أخريين:

d2ydx2 : والذي سيمثل المشتق الثاني:

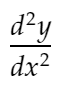
Distance_dydx: لتمثيل المسافة بين قيمة dy / dx بين نقطتين متجاورتين

هذا هو الكود الكامل للمشتق الثاني:

بعد حساب dydx في الحلقة for ، ننفذ حلقة أخرى لحساب المشتق الثاني. مع بعض الترميز الحكيم ، يمكننا حساب المشتق الثاني في نفس الحلقة (حاول كتمرين) - لكنني أبقيتهم منفصلين هنا للتوضيح.

لاحظ أيضًا أن:

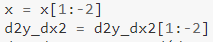
كما فعلنا في المشتق الأول ، نحذف بعض القيم هنا أيضًا. تم حذف القيمتين الأخيرتين نظرًا لأن الثانية من الأخيرة تتطلب آخر قيمة "مشتق أول" ، والتي لا يمكننا حسابها (نظرًا لعدم توفر قيمة y المطلوبة لها - كما هو موضح أعلاه). هل يعني ذلك أنه يتعين علينا حذف آخر 3 قيم في حالة المشتق الثالث؟ 🤔 - هذا لتجده.

هنا هو الرسم البياني الناتج:

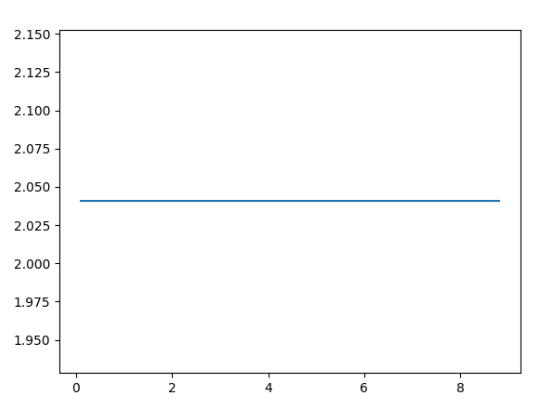
ما الذي نراه هنا؟

كما تعلم من المدرسة الثانوية:

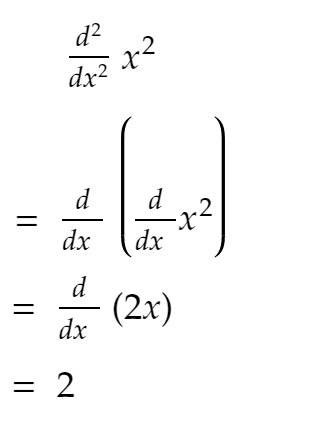
الآن ، كما ترى من الكود أعلاه ، يظل المشتق الثاني ثابتًا في الغالب ، وإذا واصلت زيادة SIZE - فإنه يقترب من 2!

لماذا معدل التغيير مهم

قد تتساءل:

- لماذا نجتاز كل هذه المشاكل السيئة؟ ما هي المعلومات المفيدة التي نحصل عليها من معدل التغيير أو المشتق؟

- لماذا لا نذهب فقط مع معدل التغيير بأي مبلغ؟ لماذا صغير فقط اللامتناهي؟ ما هي المعلومات التي نحصل عليها من معدل التغيير فيما يتعلق بالقيم اللامحدودة في الصغر ، والتي لا يمكن العثور عليها من معدل التغيير فيما يتعلق بالقيم الأكبر؟

- هذا الشيء الصغير للغاية يشبه الاختراق؟ لقد عملنا مع بعض الأعداد الصغيرة أعلاه - ولكن بالتأكيد ليست صغيرة جدًا في الواقع.

إذا سمحت لنفسي بالاستمرار ، فستبتعد عن مشاهدة طول هذا المقال ولن تصل إلى هذا الحد. ربما سنتناول هذه الأسئلة يومًا ما 😀.