إحصائيات بايز: تمهيدي سريع وخالي من الضجيج لمختبر A / B
نشرت: 2022-06-23
ما مدى ثقتك في قدرتك على تفسير النتائج التي توفرها أداة اختبار A / B الخاصة بك؟
لنفترض أنك تستخدم أداة مبنية على إحصائيات Bayesian ، وقد أخبرك أن "B" لديها فرصة بنسبة 70٪ للفوز على "A" لذا فإن "B" هو الفائز. هل تعرف ما يعنيه ذلك وكيف يجب أن يوجه إستراتيجية CRO الخاصة بك؟
في هذه المقالة ، ستتعرف على أساسيات إحصائيات Bayesian التي ستساعدك على استعادة السيطرة على اختبار A / B الخاص بك ، بما في ذلك
- عرض غير متحيز لإحصاءات بايزي
- المتكرر مقابل مزايا وعيوب بايزي
- الإعداد الذي تحتاجه لتفسير واستخدام نتائج اختبار Bayesian A / B بثقة مع تجنب بعض مصائد الأساطير الشائعة.
- ما هي إحصائيات بايزي؟
- قصة أصل بايزي
- مثال على الإحصاء البايزي المطبق على اختبار أ / ب
- مسرد قصير للمصطلحات البايزية التي تهم مختبري أ / ب
- الاستدلال بايزي
- احتمال مشروط
- توزيع الاحتمالية / توزيع الاحتمالية
- توزيع المعتقدات المسبقة
- الاقتران
- اقتران Priors
- فقدان وظيفة
- ما هي الإحصائيات المتكررة؟
- بايزي مقابل اختبار أ / ب المتكرر
- الإطار المتكرر
- إطار بايزي
- ما الذي تخبرك به إحصائيات بايز في اختبار أ / ب؟
- احتمال أن تكون الأفضل (P2BB)
- الارتفاع المتوقع
- الخسارة المتوقعة
- أساطير حول إحصاءات بايز يجب تجنبها
- الأسطورة رقم 1: يقول البايزيون افتراضاتهم ، والمتكررون لا يفعلون ذلك
- الأسطورة رقم 2. تمنحك طرق بايزي الإجابات التي تريدها بالفعل
- الأسطورة رقم 3: الاستدلال البايزي يساعدك على توصيل عدم اليقين بشكل أفضل من الاستدلال المتكرر
- الأسطورة رقم 4. نتائج اختبار Bayesian A / B محصنة ضد النظر
- الأسطورة رقم 5. الإحصائيات المتكررة غير فعالة حيث يجب عليك الانتظار لحجم عينة ثابت
- لذا ، هل يجب عليك اختيار بايزي أم التكرار؟ هناك مكان لكليهما.
- مفتاح الوجبات الجاهزة
مستعد؟ هيا لنبدأ مع الأساسيات.
ما هي إحصائيات بايزي؟
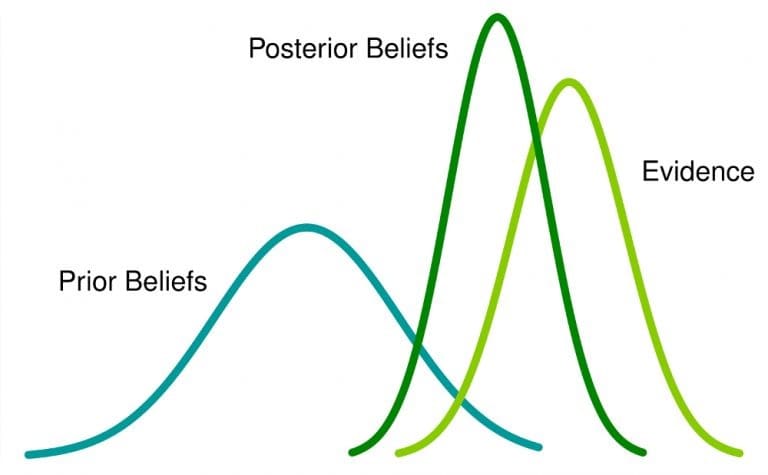
إحصائيات بايز هي طريقة للتحليل الإحصائي تعتمد على نظرية بايز ، التي تُحدِّث المعتقدات حول الأحداث حيث يتم جمع بيانات أو أدلة جديدة حول تلك الأحداث. هنا ، الاحتمال هو مقياس للاعتقاد بحدوث حدث.
ماذا يعني هذا: إذا كان لديك اعتقاد سابق بحدث ما ، وحصلت على مزيد من المعلومات المتعلقة به ، فسوف يتغير هذا الاعتقاد (أو على الأقل يتم تعديله) إلى معتقد لاحق .
هذا مفيد لفهم عدم اليقين أو عند العمل مع الكثير من البيانات الصاخبة ، مثل تحسين معدل التحويل للتجارة الإلكترونية والتعلم الآلي.
دعونا نتخيل هذا:
لنفترض ، على سبيل المثال ، أنك تشاهد سباق عربة بقالة في الكلية ، ثم يتحداك أحد المتفرجين المتحمسين للمراهنة على فوز المتأنق بالقميص الأحمر الذي يركب السيدة التي ترتدي قميصًا أخضر. تفكر في الأمر وتواجه أن الرجل ذو السترة السوداء والفتاة السوداء ذات القلنسوة سيفوزان بدلاً من ذلك.

متفرج آخر فوق رأسك ويهمس بقشيش لك ، "لقد فاز صاحب القميص الأحمر في آخر 3 سباقات من أصل 4." ماذا يحدث لرهانك؟ أنت لست متأكدًا بعد الآن ، أليس كذلك؟
لنفترض أنك علمت أيضًا أنه في المرة الأخيرة التي ارتدى فيها رجل السترة السوداء نظارته الشمسية المحظوظة ، فاز. وفي الأوقات التي لم يرتدها ، فاز رجل القميص الأحمر.
اليوم ، ترى رجل السترة السوداء يرتدي تلك النظارات. إيمانك يتغير مرة أخرى. لديك الآن ثقة أكبر في رهانك ، أليس كذلك؟ في هذه القصة ، قمت بتحديث معتقداتك في كل مرة تحصل فيها على دليل على بيانات جديدة. هذا هو النهج البايزي.
قصة أصل بايزي
عندما فكر القس توماس بايز لأول مرة في نظريته ، لم يعتقد أنها تستحق النشر. لذلك ، بقيت في ملاحظاته لأكثر من عقد. عندما طلبت عائلته من ريتشارد برايس مراجعة ملاحظاته اكتشف برايس الملاحظات التي شكلت أساس نظرية بايز.
بدأت بتجربة فكرية لبايز. لقد فكر في الجلوس وظهره على طاولة مربعة ومسطحة تمامًا وجعل مساعده يرمي كرة على الطاولة.
يمكن أن تهبط الكرة في أي مكان على الطاولة ، لكن بايز اعتقد أنه يستطيع تخمين المكان من خلال تحديث تخميناته بمعلومات جديدة. عندما سقطت الكرة على الطاولة ، سيطلب من المساعد أن يخبره إذا سقطت يسارًا أو يمينًا ، أمام أو خلف المكان الذي سقطت فيه الكرة السابقة.
وأشار إلى ذلك واستمع مع سقوط المزيد من الكرات على الطاولة. بمعلومات إضافية مثل هذه ، وجد أنه يستطيع تحسين دقة تخميناته مع كل رمية. جلب هذا فكرة تحديث فهمنا حيث حصلنا على المزيد من الأدلة من الملاحظة.
يتم تطبيق نهج Bayesian لتحليل البيانات في مختلف المجالات مثل العلوم والهندسة ، وحتى يشمل الرياضة والقانون.
في التجارب العشوائية التي يتم التحكم فيها عبر الإنترنت ، وتحديدًا اختبار A / B ، يمكنك استخدام نهج Bayesian في 4 خطوات:
- حدد التوزيع المسبق الخاص بك.
- اختر نموذجًا إحصائيًا يعكس معتقداتك.
- قم بتشغيل التجربة.
- بعد الملاحظة ، حدِّث معتقداتك واحسب التوزيع اللاحق.
تقوم بتحديث معتقداتك باستخدام مجموعة من القواعد تسمى خوارزمية بايز.
مثال على الإحصاء البايزي المطبق على اختبار أ / ب
دعنا نوضح مثال اختبار Bayesian A / B.
تخيل أننا أجرينا اختبار A / B بسيطًا على زر CTA لمتجر Shopify. بالنسبة إلى "A" ، نستخدم "Add to Cart" و "B" ، نستخدم "Add to Your Basket".
إليك كيفية إجراء المتكرر للاختبار.
هناك عالمان بديلين: أحدهما لا يختلف A و B ، لذلك لن يظهر الاختبار أي اختلاف في معدل التحويل. هذه هي الفرضية الصفرية. وفي العالم الآخر ، هناك فرق ، لذا فإن أداء أحد الأزرار أفضل من الآخر.
سيفترض المتكرر أننا نعيش في العالم 1 حيث لا يوجد فرق في أزرار الحث على الشراء ، أي بافتراض صحة الفرضية الصفرية. وبعد ذلك سيحاولون إثبات هذا الخطأ إلى مستوى محدد مسبقًا من اليقين يسمى مستوى الأهمية.
ولكن هذه هي الطريقة التي سيتعامل بها بايزي مع نفس الاختبار:
يبدأون باعتقاد مسبق بأن كلا الزرين A و B لهما فرص متساوية لإنتاج معدل تحويل بين 0 و 100٪. لذلك ، هناك مساواة زر خارج البوابة مباشرة - كلاهما لديه فرصة بنسبة 50٪ ليكونا الأفضل أداء.
ثم يبدأ الاختبار ويتم جمع البيانات. من خلال مراقبة المعلومات الجديدة ، سيقوم مختبرو Bayesian A / B بتحديث معرفتهم. لذلك ، إذا أظهر B وعدًا ، فيمكنه الوصول إلى اعتقاد لاحق بناءً على تلك الملاحظة التي تقول ، "B لديه فرصة بنسبة 61٪ للتغلب على A".
هناك اختلافات جوهرية بين الطريقتين.
لهذا السبب من المهم بالنسبة لنا الحفاظ على نهج غير متحيز لاختبار Bayesian A / B.
تتخذ معظم أدوات اختبار Bayesian A / B - ربما لأغراض تسويقية - موقفًا متطرفًا مناهضًا للتكرار وتدفع بالحجة القائلة بأن Bayesian أفضل في إخبارك بالمتغير الأكثر "ربحية".
ولكن هل يمتلك أي نهج إحصائي منفرد لاختبار أ / ب الحقوق الحصرية للرؤى؟
إذا دفع المرء بحجة بايز إلى أبعد من ذلك ، فقد يواجه دراسات حيث يقول المستجيبون إنهم يريدون معرفة أفضل مسار للعمل أو أنهم يريدون تعظيم الأرباح أو شيء مشابه. هذا يضع السؤال بحزم في منطقة نظرية القرار - وهو شيء لا يمكن أن يكون للاستدلال البايزي ولا الاستدلال المتكرر رأي مباشر فيه.
جورجي جورجييف ، مبتكر Analytics-toolkit.com ومؤلف "الأساليب الإحصائية في اختبار أ / ب عبر الإنترنت"
سنلقي نظرة سريعة على هذه التفاصيل في الأقسام المقبلة. في الوقت الحالي ، دعنا نجعل بقية هذا التمهيدي سهل الفهم.
مسرد قصير للمصطلحات البايزية التي تهم مختبري أ / ب
الاستدلال بايزي
يعمل الاستدلال البايزي على تحديث احتمالية فرضية ببيانات جديدة. إنها مبنية على المعتقدات والاحتمالات.
يعزز الاستدلال البايزي الاحتمال الشرطي لمساعدتنا على فهم كيفية تأثير البيانات على معتقداتنا. لنفترض أننا بدأنا باعتقاد مسبق بأن السماء حمراء. بعد النظر في بعض البيانات ، سرعان ما ندرك أن هذا الاعتقاد السابق خاطئ. لذلك ، نقوم بإجراء تحديث بايزي لتحسين نموذجنا غير الصحيح حول لون السماء ، وينتهي بنا الأمر باعتقاد لاحق أكثر دقة .
مايكل بيرك في نحو علوم البيانات
احتمال مشروط
الاحتمال الشرطي هو احتمال وقوع حدث بالنظر إلى وقوع حدث آخر. أي احتمال A تحت الشرط B.
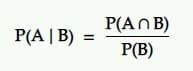
الترجمة: احتمالية حدوث حدث A نظرًا لحدث آخر B يساوي احتمالية حدوث B و A معًا مقسومًا على احتمال وقوع الحدث B.
توزيع الاحتمالية / توزيع الاحتمالية
توزيعات الاحتمالية هي توزيعات توضح مدى احتمالية أن تفترض بياناتك قيمة معينة.
حيث يمكن أن تفترض بياناتك قيمًا متعددة ، على سبيل المثال ، فئة مثل الألوان التي يمكن أن تكون رمادية أو حمراء أو برتقالية أو زرقاء ، وما إلى ذلك ، فإن التوزيع الخاص بك متعدد الحدود. بالنسبة لمجموعة من الأرقام ، قد يكون التوزيع طبيعيًا. وبالنسبة لقيم البيانات التي يمكن أن تكون نعم / لا أو صواب / خطأ ، ستكون ذات الحدين.
توزيع المعتقدات المسبقة
أو التوزيع الاحتمالي المسبق ، الذي يُسمى ببساطة سابقًا ، يعبر عن إيمانك قبل أن تحصل على دليل على بيانات جديدة. لذلك ، فهو تعبير عن اعتقادك الأولي الذي ستقوم بتحديثه بعد النظر في بعض الأدلة باستخدام تحليل بايزي (أو الاستدلال).
الاقتران
بادئ ذي بدء ، يشير المترافق إلى الانضمام معًا ، عادةً في أزواج. في نظرية الاحتمالات البايزية ، يفترض الاقتران أن السابق مترافق مع الاحتمال.
إذا كان للخلف نفس الشكل الوظيفي مثل السابق ، فإن السابق يكون مترافقًا مع وظيفة الاحتمال. يوضح هذا كيف تقوم وظيفة الاحتمالية بتحديث التوزيع السابق.
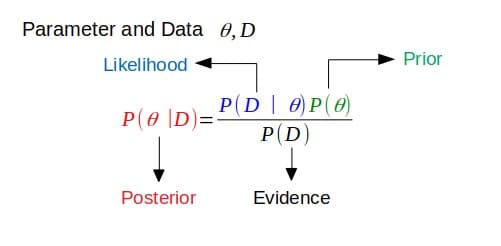
اقتران Priors
هذا مرتبط بالتعريف أعلاه. إذا كان اللاحق في نفس عائلة توزيع الاحتمالات (أو له نفس الشكل الوظيفي) مثل التوزيع الاحتمالي السابق ، فإن التوزيعات السابقة واللاحقة هي توزيعات مترافقة. في هذه الحالة ، يسمى السابق بالمقارن السابق لوظيفة الاحتمال.
يمكن أن تكون ذاتية (بناءً على معرفة المجرب) ، وموضوعية وغنية بالمعلومات (بناءً على البيانات التاريخية) ، أو غير إعلامية.
فقدان وظيفة
دالة الخسارة هي طريقة لتقدير الخسارة بقياس مدى سوء تقديرنا الحالي. يساعدنا في تقليل الخسارة في اختبار الفرضيات ، خاصة عند التعبير عن استنتاج يكمن في مجموعة من القيم المحتملة ، ويدعم اتخاذ القرار بنتائج الاختبار الخاصة بنا.
الآن هذا بعيد المنال ، يمكننا المضي قدمًا.
إذا كنت موجودًا في المنطقة منذ فترة ، فمن المحتمل أن تكون قد صادفت أكثر من عدد قليل من الميمات الإحصائي المتكرر مقابل Bayesian.

يبدو أن كلا الجانبين يبحث عن إجابات من اتجاهين متعاكسين ، لكن هل هذا هو الحال حقًا؟ لفهم هذا بشكل أفضل (مع عدم التحيز) ، دعنا نزور معسكر المتكرر.
ما هي الإحصائيات المتكررة؟
هذا هو الأسلوب الاستنتاجي الأول الذي يتعلمه معظم الناس في الإحصاء. تحسب الإحصائيات المتكررة احتمالية حدوث حدث (فرضية) بشكل متكرر في ظل نفس الظروف.
يتبع اختبار فرضية أ / ب باستخدام النهج التكراري الخطوات التالية:
- أعلن بعض الفرضيات. عادةً ما تكون الفرضية الصفرية هي أن المتغير الجديد "ب" ليس أفضل من "أ" الأصلي بينما تعلن الفرضية البديلة عكس ذلك.
- حدد حجم العينة مقدمًا باستخدام حساب القوة الإحصائية ، إلا إذا كنت تستخدم أساليب اختبار متسلسلة. استخدم حاسبة حجم العينة التي تأخذ في الاعتبار القوة الإحصائية ومعدل التحويل الحالي والحد الأدنى من التأثير القابل للاكتشاف.
- قم بإجراء الاختبار وانتظر حتى يتم تعريض كل شكل لحجم العينة المحدد مسبقًا.
- احسب احتمالية ملاحظة نتيجة ما على الأقل بنفس القدر من البيانات الموجودة تحت الفرضية الصفرية (القيمة p). ارفض فرضية العدم وانشر المتغير الجديد للإنتاج إذا كانت القيمة p <5٪.
كيف يقارن هذا مع بايزي؟ دعونا نرى…
بايزي مقابل اختبار أ / ب المتكرر
هذا نقاش سيء السمعة في أي مكان يتم فيه استخدام الاستدلال الإحصائي. ولكي أكون صريحا ، هذا لا طائل من ورائه. كلاهما له مزاياهما وحالاتهما حيث يكونان أفضل طريقة للاستخدام.
على عكس ما يعتقده معظم المروجين في كلا المعسكرين ، فإنهم متشابهون في عدة نواحٍ ولا يقترب أي منهما من الحقيقة من الآخر - على الرغم من اختلاف مقاربتهم.
عند تطبيقها على اختبار A / B ، على سبيل المثال ، لن تمنحك أي طريقة محددة تنبؤًا مطلقًا ودقيقًا من حيث مسار العمل الذي سيؤدي إلى نمو الأعمال. بدلاً من ذلك ، يساعدك اختبار A / B على إزالة المخاطر من عملية اتخاذ القرار.
بغض النظر عن كيفية تحليل بياناتك - باستخدام نهج بايزي أو متكرر - يمكنك القيام بحركات بمستوى معين من اليقين أنك على صواب.
ولهذا السبب ، كلا النموذجين الإحصائيين صالحين. قد يتمتع Bayesian بميزة السرعة ولكنه يتطلب حسابًا أكثر من المتكرر.
تحقق من الاختلافات الأخرى ...
الإطار المتكرر
معظمنا على دراية بالنهج المتكرر من دورات الإحصاء التمهيدية. لقد حددنا المنهجية أعلاه - من إعلان الفرضية الصفرية ، وتحديد حجم العينة ، وجمع البيانات عبر تجربة عشوائية ، وأخيراً مراقبة نتيجة ذات دلالة إحصائية.
في التكرار ، نعتبر الاحتمال مرتبطًا بشكل أساسي بترددات الأحداث المتكررة. لذلك ، في رمي العملة العادلة ، يعتقد المتكرر أنه إذا خمنوا بشكل متكرر بما فيه الكفاية ، فسيحصلون على الوجه الصحيح بنسبة 50 ٪ من الوقت ونفس الشيء بالنسبة للذيول.
العقلية المتكررة: "إذا كررت التجربة في نفس الظروف مرارًا وتكرارًا ، فما هي فرص حصول طريقي على الإجابة الصحيحة؟"
إطار بايزي
بينما يعامل النهج التكراري معلمة السكان لكل متغير على أنه ثابت (غير معروف) ، فإن نهج بايز يصمم كل قيمة معلمة كمتغير عشوائي مع بعض توزيع الاحتمالات.
هنا ، تقوم بحساب التوزيعات الاحتمالية (وبالتالي القيم المتوقعة) للمعلمات ذات الأهمية مباشرة.
ومن أجل نمذجة التوزيع الاحتمالي لكل متغير ، فإننا نعتمد على قاعدة بايز لدمج نتائج التجربة مع أي معرفة سابقة لدينا حول مقياس الاهتمام. يمكننا تبسيط العمليات الحسابية باستخدام مرافق سابق.
لخص أليكس بيركيت خوارزمية بايز بهذه الطريقة:
- حدد التوزيع السابق الذي يدمج معتقداتك الشخصية حول المعلمة. يمكن أن يكون السابق غير إعلامي أو مفيد.
- اجمع البيانات.
- قم بتحديث توزيعك السابق بالبيانات باستخدام نظرية بايز (على الرغم من أنه يمكنك الحصول على طرق بايز بدون استخدام صريح لقاعدة بايز - راجع بايزي غير المعياري) للحصول على التوزيع اللاحق. التوزيع اللاحق هو توزيع احتمالي يمثل معتقداتك المحدثة حول المعلمة بعد رؤية البيانات.
- تحليل التوزيع اللاحق ولخصه (متوسط ، متوسط ، sd ، مقاييس ...).
باختصار ، يركز مجرب بايزي على منظورهم الخاص وما يعنيه الاحتمال بالنسبة لهم. رأيهم يتطور مع البيانات المرصودة. من ناحية أخرى ، يعتقد المتكررون أن الإجابة الصحيحة موجودة في مكان ما.

افهم أن الجدل المتكرر مقابل البايزي لا يؤثر كثيرًا على تحليل اختبار A / B. ترتبط الاختلافات الرئيسية بين المعسكرين بشكل أكبر بما يمكن اختباره.
لا يتم استخدام إحصائيات الاحتمالات بشكل عام إلى حد كبير في التحليل اللاحق. تعتبر حجة Bayesian-Frequentist أكثر قابلية للتطبيق فيما يتعلق باختيار المتغيرات التي سيتم اختبارها في نموذج A / B ، ولكن حتى هناك ، ينتهك معظم مختبري A / B الجحيم من فرضيات البحث ، والاحتمالات ، وفترات الثقة .
دكتور روب بالون إلى CXL
يوضح جورجي كذلك:
هناك العديد من حاسبات بايزي على الإنترنت وبائع برمجيات اختبار أ / ب رئيسي واحد على الأقل يطبق محركًا إحصائيًا بايزي يستخدم جميعها ما يسمى ببايز غير إعلامي (قليل من التسمية الخاطئة ، لكن دعونا لا نتعمق في هذا). في معظم الحالات ، تتطابق نتائج هذه الأدوات عدديًا مع نتائج اختبار متكرر على نفس البيانات. لنفترض أن أداة Bayesian ستبلغ عن شيء مثل "احتمالية 96٪ أن B أفضل من A" بينما الأداة المتكررة ستنتج قيمة p 0.04 والتي تقابل مستوى ثقة 96٪.
في موقف مثل ما سبق ، وهو أكثر شيوعًا مما يرغب البعض في الاعتراف به ، ستؤدي كلتا الطريقتين إلى نفس الاستدلال وسيكون مستوى عدم اليقين هو نفسه ، حتى لو كان التفسير مختلفًا.
ماذا سيقول بايزي عن هذه النتيجة؟ هل يحول القيمة الاحتمالية إلى احتمال لاحق مناسب عند عرض سيناريو لا توجد فيه معلومات مسبقة؟ أم أن جميع تطبيقات اختبارات بايزي مضللة لاستخدامها مسبقًا غير إعلامية في حد ذاتها؟
ليست هناك حاجة حقًا لاختيار معسكر والعثور على مكان خلف الملجأ لرمي الحجارة على المعسكر الآخر. حتى أن هناك دليلًا على أن كلا الإطارين يؤديان إلى نفس النتائج. بغض النظر عن الطريق الذي تختاره ، من المحتمل أن تكون الوجهة هي نفسها. يعتمد ذلك على كيفية الوصول إلى هناك باستخدام Frequentist vs Bayesian.
على سبيل المثال:
- هناك بيانات تُظهر أن اختبار Bayesian أسرع والخيار المفضل للتجارب التفاعلية:
نظرًا لأن نموذج Bayesian يسمح للقائمين بالتجربة بتحديد المعتقد رسميًا ودمج المعرفة الإضافية ، فهو أسرع من التحليل الإحصائي التقليدي.
في محاكاة اختبار Bayesian A / B ، عندما تم تعديل معيار القرار (أي زيادة التسامح مع الأخطاء) ، انتهى 75٪ من التجارب في حدود 22.7٪ من الملاحظات المطلوبة بالنهج التقليدي (عند مستوى أهمية 5٪). وسجل خطأ بنسبة 10٪ فقط من النوع الثاني. - يعتبر Bayesian أيضًا أكثر تسامحًا ، بينما المتكرر يتجنب المخاطرة:
في حين أن العديد من الاختبارات المتكررة تستخدم دلالة إحصائية تبلغ 95٪ ، يمكن أن يرضي Bayesians بأقل من ذلك. إذا كان لدى المتغير فرصة بنسبة 78٪ للتغلب على عنصر التحكم ، اعتمادًا على الخسارة المتوقعة ، فقد يكون قرارًا سليمًا "نشر هذا المتغير".
إذا كنت مخطئًا وكانت الخسارة المتوقعة أقل من نسبة مئوية ، فهذا ضرر ضئيل جدًا للعديد من الشركات. قد يكون هذا النهج غير المستقر أكثر ملاءمة لاتخاذ القرار السريع في سيناريوهات منخفضة المخاطر للغاية. - ومع ذلك ، فإن عمليات المحاكاة والحسابات البايزية ثقيلة الحساب:
المتكرر ، من ناحية أخرى ، يعتمد على القلم والورق. تحذير: إذا كانت أداة اختبار A / B الخاصة بك تستخدم Bayesian ولا تعرف الافتراضات التي تتم إضافتها إلى بياناتك ، فلا يمكنك الاعتماد على "الإجابة" التي يقدمها لك البائع. خذها بحفنة ملح. وقم بإجراء تحليلك الخاص.
ليس كل شيء مشمس وأقواس قزح مع بايزي. مثلما يشير جورجي بقائمة الأسئلة هذه:
- "هل ترغب في الحصول على ناتج دالة الاحتمال السابق ودالة الاحتمال؟"
- "هل تريد مزيجًا من الاحتمالات السابقة والبيانات كمخرجات؟"
- "هل تريد المعتقدات الذاتية الممزوجة بالبيانات لإنتاج المخرجات؟" (في حالة استخدام معلومات مسبقة)
- "هل ستشعر بالراحة عند تقديم الإحصاءات التي توجد فيها معلومات سابقة يُفترض أنها على درجة عالية من اليقين مختلطة مع البيانات الفعلية؟"
هذه كلها جوانب من إحصائيات بايز ، من منظور الشخص العادي.
ما الذي تخبرك به إحصائيات بايز في اختبار أ / ب؟
لقد صممت اختبار A / B الخاص بك لإعطاء نظرة ثاقبة حول كيفية تأثير التغيير على مقياس الاهتمام الخاص بك ، مثل معدل التحويل أو العائد لكل زائر.
عند استخدام أداة تعمل مع إحصائيات Bayesian ، من المهم أن تفهم ما تعنيه نتائجك لأن "B هو الفائز" لا يعني بالضبط ما يعتقده معظم الناس.
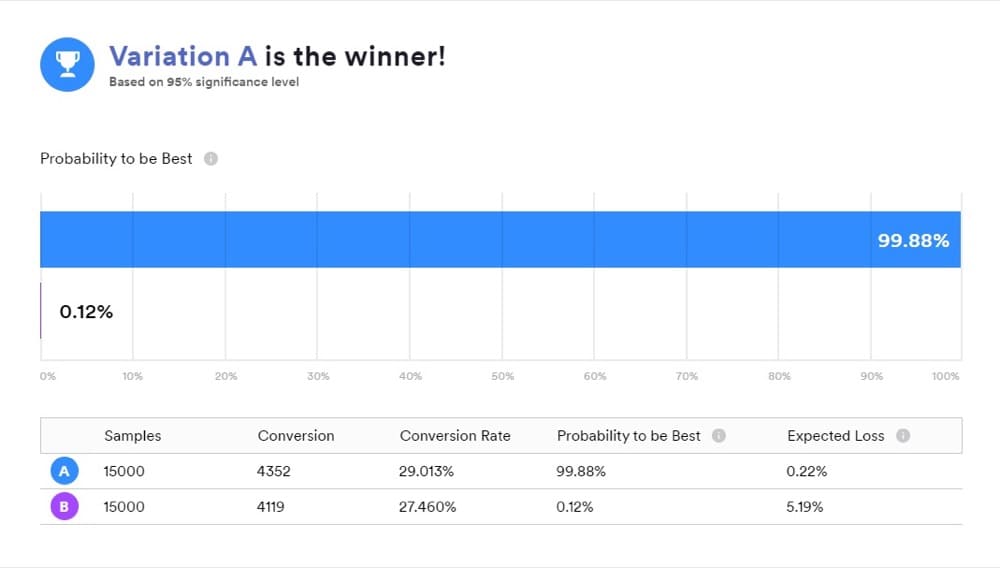
إنها طريقة ملائمة لتقديم النتائج ، لكن هذا لم يكشف عنه اختبارك. بدلاً من ذلك ، الإجابات التي تريدها هي في مقارنات لاحقة بين "أ" و "ب".
فيما يلي 3 طرق للمقارنة:
احتمال أن تكون الأفضل (P2BB)
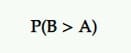
هذا هو الاحتمال الذي يعلن الفائز في اختبار Bayesian A / B.
المتغير الذي يحتمل أن يكون الأفضل هو المتغير ذو أعلى احتمالية للاستمرار في التفوق على الآخر.
يتم حساب هذا من مجموعة من العينات اللاحقة لمقياس الفائدة من الأصل والمتحدي.
لذلك ، إذا كان لدى B أعلى احتمال لزيادة معدلات التحويل الخاصة بك ، على سبيل المثال ، يتم إعلان B الفائز.
الارتفاع المتوقع
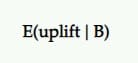
لذا ، إذا كان B هو الفائز ، فما مقدار الارتفاع الذي يجب أن نتوقعه منه؟ هل سيستمر في تقديم نفس النتائج التي رأيناها في الاختبار؟
هذه هي البصيرة التي يسعى الارتفاع المتوقع لتوفيرها. يُعرَّف الارتفاع المتوقع في اختيار B على A ، بالنظر إلى مجموعة من العينات الخلفية ، بأنه الفاصل الزمني الموثوق (أو المتوسط) للزيادة المئوية.
في اختبار A / B ، عادة ما نقارن هذا بين المتحدي والسيطرة. لذلك ، إذا خسر المنافس ، يتم تمثيله بقيم سالبة (مثل -11.35٪) وقيم موجبة (مثل + 9.58٪) إذا فاز.
الخسارة المتوقعة
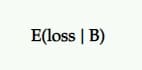
نظرًا لعدم وجود احتمال بنسبة 100٪ أن يكون B أفضل من A ، فهناك فرصة لتسجيل خسارة إذا اخترت B على A. ويتم تمثيل ذلك كخسارة متوقعة ، وكما هو الحال مع الارتفاع المتوقع ، يتم التعبير عنه من وجهة نظر المنافس ضد السيطرة.
يخبرك بمخاطر اختيار متغير P2BB (أي الفائز المعلن).
قبل أن نغوص في الأساطير ، شكراً جزيلاً لأسطورة التحليلات جورجي جورجييف. ألهمت تحليلاته المتعمقة للاستدلال المتكرر مقابل الاستدلال البايزي واحتمالية Bayesian والإحصاءات في اختبار A / B القسم التالي.
أساطير حول إحصاءات بايز يجب تجنبها
مع وجود تنافس قديم بقدر ما لا داعي له ، فقد جمعت مناقشة Bayesian vs Frequentist الكثير من المدخلات - وأعطت ارتفاعًا إلى الكثير من الأساطير.
يتم الترويج لأكبر هذه الخرافات (الأسطورة رقم 2) بواسطة بائعي أدوات اختبار A / B لإخبارك لماذا يكون أحد الأساليب أفضل من الآخر.
لكن بعد قراءة الأقسام أعلاه ، فأنت تعلم بشكل أفضل.
دعونا نكشف الثغرات في هذه الأساطير.
الأسطورة رقم 1: يقول البايزيون افتراضاتهم ، والمتكررون لا يفعلون ذلك
يشير هذا إلى أن Bayesians يضعون افتراضات في شكل توزيعات سابقة وهي مفتوحة للتقييم. لكن المتكررون يضعون افتراضات مخفية في منتصف الرياضيات.
لماذا هو خطأ: يقوم البايزيون والمتكررون بافتراضات أساسية مماثلة ، والفرق الوحيد هو أن البايزيين يضعون افتراضات إضافية - فوق الرياضيات.
تستخدم النماذج المتكررة الافتراضات في الرياضيات ، مثل شكل التوزيع ، والتجانس أو عدم التجانس للتأثير عبر الملاحظات ، واستقلالية الملاحظة. وهم ليسوا مخفيين. في الواقع ، تمت مناقشتها على نطاق واسع في المجتمع الإحصائي وتم ذكرها في كل اختبار إحصائي متكرر.
الحقيقة: يذكر المتكررون افتراضاتهم صراحة ويأخذونها خطوة أخرى إلى الأمام لاختبار الافتراضات: اختبارات الحالة الطبيعية واختبار جودة الملاءمة (والتي بموجبها لدينا اختبار عدم تطابق نسبة العينة) والمزيد.
الأسطورة رقم 2. تمنحك طرق بايزي الإجابات التي تريدها بالفعل
المفهوم الخاطئ هنا هو أن قيم p وفواصل الثقة لا تخبر المختبرين بما يريدون معرفته ، في حين أن الاحتمالات اللاحقة والفترات الزمنية الموثوقة تفعل ذلك. يريد الناس معرفة أشياء مثل
- احتمال تفوق B على A و
- احتمالية أن النتيجة ليست صدفة.
لا توفر اختبارات القيم P والفرضيات (الاستدلال المباشر) هذه المعلومات ، ولكن الاستدلال العكسي يفعل ذلك.
لماذا هي خاطئة: هذه مسألة لغويات. بشكل عام ، عندما يستخدم غير الإحصائيين مصطلحات مثل "الاحتمالية" و "الصدفة" و "الاحتمال" ، فإنهم لا يستخدمونها مع وضع معناها التقني في الاعتبار. تحقق بشكل أعمق وستجد أنهم مرتبكون بشأن الاستدلال العكسي كما هو الحال مع الاستدلال المباشر.
وفقًا لجورجي جورجييف ، تبدأ أسئلة مثل هذه في الظهور:
- " ما هو الاحتمال المسبق؟ ما هي القيمة التي تجلبها؟ "
- "ما هي وظيفة الاحتمال؟"
- "ما هو الاحتمال" السابق "، ليس لدي بيانات سابقة؟"
- "كيف أدافع عن خيار الاحتمال السابق؟"
- "هل هناك طريقة لإيصال ما تقوله البيانات فقط ، بدون أي من هذه الخلطات؟"
الحقيقة: يجب أن يكون هناك فهم أفضل لما يريد المختبرين معرفته ، وليس على سوء تفسيرهم للمصطلحات الفنية. تخبرك قيم P وفواصل الثقة وغيرها بمدى دقة فحص النتائج مع البيانات التي تم جمعها. لقد وفروا قدرًا من اليقين دون تأثير الافتراضات السابقة غير الموضوعية وغير المختبرة.
الأسطورة رقم 3: الاستدلال البايزي يساعدك على توصيل عدم اليقين بشكل أفضل من الاستدلال المتكرر
لأن نتائج الاختبارات تنتج رؤى أكثر "ذات مغزى".
لماذا هو خطأ: كلا النهجين المتكرر والبايزي لهما أدوات متشابهة لمساعدتك على إيصال اليقين ونتائج اختبار أ / ب الخاص بك.
| كثرة | بايزي | ||||||||||
| ● تقديرات النقاط | ● تقديرات النقاط | ||||||||||
| ● قيم ف | ● فترات ذات مصداقية | ||||||||||
| ● فترات الثقة | ● عوامل بايز | ||||||||||
| ● منحنيات القيمة P | ● التوزيعات الخلفية (إنجاز نفس المهمة كمنحنيات متكررة) | ||||||||||
| ● منحنيات الثقة | |||||||||||
| ● منحنيات الخطورة ، إلخ. |
الحقيقة: كل هذا يتوقف على كيفية استخدامها. كلا الطريقتين لهما نفس القدر من الفعالية في توصيل عدم اليقين. ومع ذلك ، هناك اختلافات في كيفية تقديمها لمقياس عدم اليقين.
الأسطورة رقم 4. نتائج اختبار Bayesian A / B محصنة ضد النظر
يجادل بعض الإحصائيين في نظرية بايز بأنه يمكنك إيقاف اختبار بايزي بمجرد أن ترى "فائزًا واضحًا" وهذا لا يحدث فرقًا كبيرًا في النتيجة النهائية.
ربما تعلم أن هذا أمر غير مقبول في الاختبارات المتكررة ، لذلك يتم احتسابه على أنه عيب عند مقارنته بايزيان. لكن هل هي حقا؟
سبب الخطأ: في دراسة أجريت عام 1969 في مجلة الجمعية الإحصائية الملكية بعنوان "اختبارات الأهمية المتكررة حول تراكم البيانات" ، أرميتاج وآخرون. أظهر كيف يؤدي التوقف الاختياري المستند إلى النتائج إلى زيادة احتمالية الخطأ.
لا يمكنك التوقف فقط عندما تلاحظ فائزًا ، وتحديث اللاحق الخاص بك ، واستخدامه كسابقك التالي دون تعديل الطريقة التي يعمل بها تحليل بايزي.
الحقيقة: نظرة خاطفة تؤثر على الاستدلال البايزي بقدر ما تؤثر على الاستدلال المتكرر (إذا كنت تريد أن تفعل ذلك بشكل صحيح).
الأسطورة رقم 5. الإحصائيات المتكررة غير فعالة حيث يجب عليك الانتظار لحجم عينة ثابت
يعتقد بعض أعضاء مجتمع CRO أنه يجب إجراء الاختبارات الإحصائية المتكررة بحجم عينة ثابت ومحدد مسبقًا ، وإلا فإن النتائج غير صالحة.
نتيجة لذلك ، أنت تنتظر وقتًا أطول من اللازم للحصول على النتائج التي تريدها.
لماذا هذا خطأ: لم يتم استخدام الإحصائيات المتكررة بهذه الطريقة منذ حوالي سبعة عقود حتى الآن. مع الاختبارات المتتابعة المتكررة ، لا تحتاج إلى مدة محددة مسبقًا.
الحقيقة: الاختبارات المتسلسلة ، الأكثر شيوعًا اليوم ، تتطلب حدًا أقصى لحجم العينة لموازنة أخطاء النوع الأول والنوع الثاني ، لكن حجم العينة الفعلي المستخدم يختلف من حالة إلى أخرى اعتمادًا على النتيجة المرصودة.
لذا ، هل يجب عليك اختيار بايزي أم التكرار؟ هناك مكان لكليهما.
ليست هناك حاجة لاختيار جانب. كلتا الطريقتين لها مكانها. على سبيل المثال ، مشروع طويل الأجل يستخدم برامج مسبقة محدثة ويحتاج إلى نتائج سريعة تتناسب بشكل أفضل مع نهج Bayesian.
الطريقة المتكررة ، من ناحية أخرى ، هي الأنسب للمشاريع التي تتطلب قدرًا كبيرًا من التكرار في نتائجها. كما هو الحال في كتابة البرامج التي سيستخدمها العديد من الأشخاص الذين لديهم العديد من مجموعات البيانات.
كما يقول كاسي كوزيركوف ، رئيس استخبارات القرار في Google ، "الإحصاء هو علم تغيير رأيك في ظل عدم اليقين".
قالت في فيديو ملخص إحصائيات بايزي مقابل إحصائيات متكررة:
"يمكنك أن تأخذ هذا الجدل المتكرر والبايزي وتحطيمه بالكامل إلى ما تغير رأيك بشأنه. يغير المتكررون رأيهم بشأن الأفعال ، ولديهم فعل افتراضي مفضل - ربما ليس لديهم أي معتقدات - لكن لديهم فعلًا يحلو لهم تحت الجهل ثم يسألون ، "هل يغير دليلي [أو بياناتي] رأيي بشأن هذا العمل؟ " "هل أشعر بالسخرية من القيام بذلك بناءً على أدلتي؟"
من ناحية أخرى ، يغير البايزيون رأيهم بطريقة مختلفة. يبدأون برأي ، رأي شخصي معبر عنه رياضيًا ، يسمى سابقًا ، ثم يسألون ، "ما هو الرأي المعقول الذي يجب أن يكون لدي بعد أن أدرج بعض الأدلة؟" وهكذا يغير المتكررون رأيهم بشأن الأفعال ، يغير البايزيون رأيهم بشأن المعتقدات.
واعتمادًا على الطريقة التي تريد بها تأطير عملية صنع القرار ، قد تفضل الذهاب مع معسكر مقابل الآخر ".
في النهاية ، نتجه جميعًا نحو استنتاجات مماثلة - يكمن الاختلاف في كيفية تقديم هذه الاستنتاجات إليك.
إذا كان الاستدلال المتكرر والاستدلال البايزي عبارة عن وظائف برمجية ، مع كون المدخلات مشاكل إحصائية ، فسيكون الاثنان مختلفين في ما يعادانه إلى المستخدم. ستعيد دالة الاستنتاج المتكرر رقمًا يمثل تقديرًا (عادةً ما يكون إحصائيًا موجزًا مثل متوسط العينة وما إلى ذلك) ، في حين أن دالة Bayesian ستعيد الاحتمالات.
مقتطف من كتاب "البرمجة الاحتمالية وطرق بايزي للقراصنة
ما هو غير صحيح تمامًا هو الادعاء بأن أحدهما يعطي نتائج عملية أكثر من الآخر.
مفتاح الوجبات الجاهزة
تتكون إحصائيات Bayesian في اختبار A / B من 4 خطوات متميزة:
- حدد التوزيع المسبق الخاص بك
- اختر نموذجًا إحصائيًا يعكس معتقداتك
- قم بتشغيل التجربة
- استخدم النتائج لتحديث معتقداتك وحساب التوزيع اللاحق
ستوجهك نتائجك نحو الاحتمالات الثاقبة. لذلك ستعرف أي المتغير لديه أعلى احتمال ليكون الأفضل ، وخسارتك المتوقعة ، والارتفاع المتوقع.
عادةً ما يتم تفسيرها لك بواسطة معظم أدوات اختبار A / B باستخدام إحصائيات Bayesian. لكن المجرب الشامل سيقوم بإجراء تحليل ما بعد الاختبار لفهم هذه النتائج بشكل أفضل.
نظرًا لأنك وصلت إلى هذا الحد ، فإليك حقيقة ممتعة لك: هل تعرف صورة توماس بايز التي يعرفها الجميع؟ هذا:

لا أحد متأكد بنسبة 100٪ أنه هو.